题目内容
若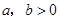 ,则
,则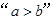 是“
是“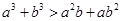 ”的( )
”的( )
A.充分非必要条件 B.必要非充分条件
C.充分且必要条件 D.既非充分也非必要条件
【答案】
A
【解析】
试题分析: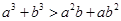
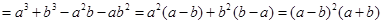 ,显然由
,显然由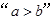 可以得出“
可以得出“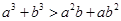 ”,反之由“
”,反之由“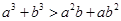 ”,不一定有
”,不一定有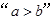 ,所以
,所以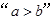 是“
是“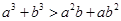 ”的充分非必要条件.
”的充分非必要条件.
考点:本小题主要考查不等式的性质和充分条件、必要条件的判断.
点评:比较大小的常用方法是作差或作商,要灵活运用,要判断充分条件、必要条件,首先要看清谁是条件谁是结论,分清楚是谁能推出谁.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


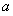
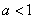

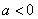
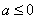
 ,若
,若 ,则
,则 是函数
是函数 在
在 处的导数值
处的导数值 ,所以
,所以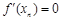 ,则
,则 是函数
是函数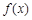 的极值
的极值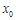 处有导数
处有导数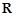 上的可导函数
上的可导函数 无实数解,则
无实数解,则 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 ,若
,若  +
+
 ,
, 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 ,若
,若 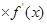 +
+
 ,
,