题目内容
计算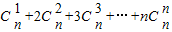 ,可以采用以下方法:构造恒等式
,可以采用以下方法:构造恒等式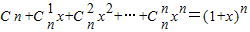 ,两边对x求导,得
,两边对x求导,得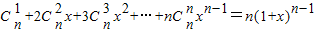 ,在上式中令x=1,得
,在上式中令x=1,得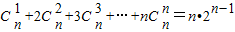 .类比上述计算方法,计算
.类比上述计算方法,计算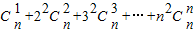 = .
= .
【答案】分析:对Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1=n(1+x)n-1,两边同乘以x整理后再对x求导,最后令x=1代入整理即可得到结论.
解答:解:对Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1=n(1+x)n-1,两边同乘以x得:
xCn1+2Cn2x2+3Cn3x3+…+nCnnxn=n•x•(1+x)n-1,
再两边对x求导
得到:Cn1+22Cn2x+32Cn3x2+…+n2Cnnxn-1=n(1+x)n-1+n(n-1)x(1+x)n-2
在上式中令x=1,得Cn1+22Cn2+32Cn3+…+n2Cnn=n•2n-1+n(n-1)•2n-2=n(n+1)2n-2.
故答案为:n(n+1)2n-2.
点评:本题主要考查二项式定理的应用.是道好题,解决问题的关键在于对Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1=n(1+x)n-1,两边同乘以x整理后再对x求导,要是想不到这一点,就变成难题了.
解答:解:对Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1=n(1+x)n-1,两边同乘以x得:
xCn1+2Cn2x2+3Cn3x3+…+nCnnxn=n•x•(1+x)n-1,
再两边对x求导
得到:Cn1+22Cn2x+32Cn3x2+…+n2Cnnxn-1=n(1+x)n-1+n(n-1)x(1+x)n-2
在上式中令x=1,得Cn1+22Cn2+32Cn3+…+n2Cnn=n•2n-1+n(n-1)•2n-2=n(n+1)2n-2.
故答案为:n(n+1)2n-2.
点评:本题主要考查二项式定理的应用.是道好题,解决问题的关键在于对Cn1+2Cn2x+3Cn3x2+…+nCnnxn-1=n(1+x)n-1,两边同乘以x整理后再对x求导,要是想不到这一点,就变成难题了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
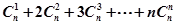 ,可以采用以下方法:
,可以采用以下方法: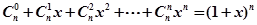 ,两边对x求导,
,两边对x求导,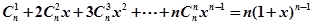 ,在上式中令
,在上式中令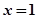 ,得
,得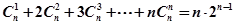 .类比上述计算方法,
.类比上述计算方法,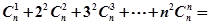 .
.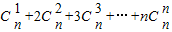 ,可以采用以下方法:构造恒等式
,可以采用以下方法:构造恒等式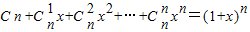 ,两边对x求导,得
,两边对x求导,得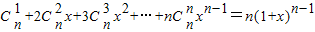 ,在上式中令x=1,得
,在上式中令x=1,得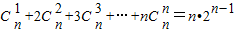 .类比上述计算方法,计算
.类比上述计算方法,计算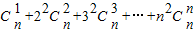 = .
= .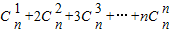 ,可以采用以下方法:构造恒等式
,可以采用以下方法:构造恒等式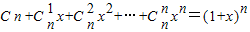 ,两边对x求导,得
,两边对x求导,得 ,在上式中令x=1,得
,在上式中令x=1,得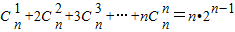 .类比上述计算方法,计算
.类比上述计算方法,计算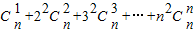 = .
= .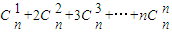 ,可以采用以下方法:构造恒等式
,可以采用以下方法:构造恒等式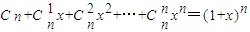 ,两边对x求导,得
,两边对x求导,得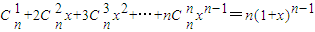 ,在上式中令x=1,得
,在上式中令x=1,得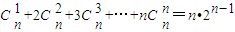 .类比上述计算方法,计算
.类比上述计算方法,计算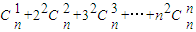 = .
= .