题目内容
点
是椭圆上的一点,
是焦点,且,则△
的面积是 .
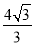
【解析】
试题分析：由余弦定理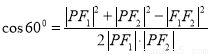
和
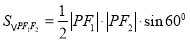联立可得：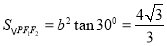
.
考点：椭圆的定义、余弦定理.
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
灵星计算小达人系列答案孟建平错题本系列答案题目内容
点是椭圆上的一点,是焦点,且,则△的面积是 .
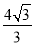
【解析】
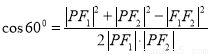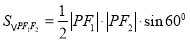试题分析：由余弦定理和联立可得：.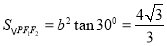
考点：椭圆的定义、余弦定理.
灵星计算小达人系列答案孟建平错题本系列答案
