题目内容
已知定义在区间[－1，1]上的函数
为奇函数。.
（1）求实数b的值。（2）判断函数
（－1，1）上的单调性，并证明你的结论。
（3）
在xÎ [ m，n ]上的值域为[ m，n ] ( –1
m < n1 )，求m+n的值。
（I）b＝0，（2）函数（－1，1）上是增函数………………4分
证明：∵
∴
………………6分
，∴
………………7分
∴函数（－1，1）上是增函数 …………8分
证法二：用定义证明
（3）由（2）知函数[m，n]上是增函数∴函数的值域为[
，
]
∴ 
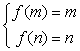即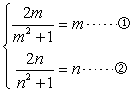
…………………………9分
由①得m = –1 或 0或1
由②得n = –1 或 0或1…………………………………………11分
又∵–1 ≤ m < n ≤ 1
∴m=–1,n=0;或m=–1,n=1;或m=0,n=1…………………12分
∴m+n=–1;或m+n=0;或m+n=1………13分
练习册系列答案
相关题目
已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1、x2，给出下列结论：
已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1，x2，下列结论正确的是（ ）
| A、f（x2）-f（x1）＞x2-x1 | ||||
| B、f（x2）-f（x1）＜x2-x1 | ||||
C、
| ||||
| D、x2f（x1）＞x1f（x2） |
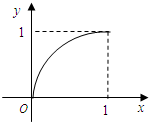已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：
.
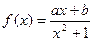为奇函数。且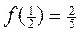
的值。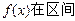
（－1，1）上是增函数。
.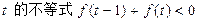