题目内容
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为 ,
,
(1)设∠CA1O = (rad),将y表示成
(rad),将y表示成 的函数关系式;
的函数关系式;
(2)请你设计 ,当角
,当角 正弦值的大小是多少时,细绳总长
正弦值的大小是多少时,细绳总长 最小,并指明此时
BC应为多长。
最小,并指明此时
BC应为多长。

【答案】
(1) (2) 当角
(2) 当角 满足
满足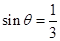 时,
时,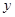 最小,最小为
最小,最小为 ;此时
;此时
【解析】
试题分析:(1)解:在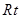 △COA1中,
△COA1中,
 ,
, , ……2分
, ……2分

 ,
……7分
,
……7分
(Ⅱ) ,
,
令 ,则
,则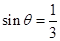 , ……10分
, ……10分
当 时,
时, ;
; 时,
时, ,
,
∵ 在
在 上是增函数,
上是增函数,
∴当角 满足
满足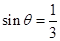 时,
时,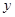 最小,最小为
最小,最小为 ;此时
;此时 .…14分
.…14分
考点:本小题主要考查利用三角函数和导数解决实际问题中的最值问题,考查学生抽象数学模型、转化问题和运算求解能力.
点评:解决实际问题,关键是从实际问题中抽象出数学模型,还要注意实际问题的定义域.

练习册系列答案
相关题目
 如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即OB)为2m,在圆环上设置三个等分点A1,A2,A3.点C为OB上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即OB)为2m,在圆环上设置三个等分点A1,A2,A3.点C为OB上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym. 如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即OB)为2m,在圆环上设置三个等分点A1,A2,A3.点C为OB上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等,求细绳总长y的最小值,并求出此时BC的长度.
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即OB)为2m,在圆环上设置三个等分点A1,A2,A3.点C为OB上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等,求细绳总长y的最小值,并求出此时BC的长度.
