题目内容
在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答对这道题的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .
.
(Ⅰ)求乙、丙两人各自回答对这道题的概率.
(Ⅱ)求甲、乙、丙三人中恰有两人回答对该题的概率.
解:记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件A、B、C,
则P(A)= ,且有
,且有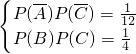 ,即
,即 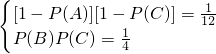 ,
,
∴P(B)= ,P(C)=
,P(C)= .…(6分)
.…(6分)
(2)由(1)P( )=1-P(A)=
)=1-P(A)= ,P(
,P( )=1-P(B)=
)=1-P(B)= .
.
则甲、乙、丙三人中恰有两人回答对该题的概率为:P=P(A•B• )+P(A•
)+P(A• •C)+P(
•C)+P( •B•C)=
•B•C)=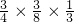 +
+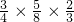 +
+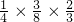 =
=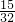 ..…(12分)
..…(12分)
分析:记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件A、B、C,根据已知的条件求出甲、乙、丙三人各自答对这道题的概率P(A)、P(B)、P(C)的值,
由所求事件的概率 P=P(A•B• )+P(A•
)+P(A• •C)+P(
•C)+P( •B•C),运算求得结果.
•B•C),运算求得结果.
点评:本题主要考查独立重复试验的概率乘法公式,互斥事件和对立事件,体现了分类讨论的数学思想,求出甲、乙、丙三人各自答对这道题的概率,是解题的关键.
则P(A)=
 ,且有
,且有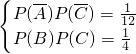 ,即
,即 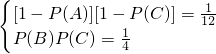 ,
,∴P(B)=
 ,P(C)=
,P(C)= .…(6分)
.…(6分)(2)由(1)P(
 )=1-P(A)=
)=1-P(A)= ,P(
,P( )=1-P(B)=
)=1-P(B)= .
.则甲、乙、丙三人中恰有两人回答对该题的概率为:P=P(A•B•
 )+P(A•
)+P(A• •C)+P(
•C)+P( •B•C)=
•B•C)=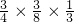 +
+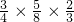 +
+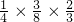 =
=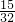 ..…(12分)
..…(12分)分析:记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件A、B、C,根据已知的条件求出甲、乙、丙三人各自答对这道题的概率P(A)、P(B)、P(C)的值,
由所求事件的概率 P=P(A•B•
 )+P(A•
)+P(A• •C)+P(
•C)+P( •B•C),运算求得结果.
•B•C),运算求得结果.点评:本题主要考查独立重复试验的概率乘法公式,互斥事件和对立事件,体现了分类讨论的数学思想,求出甲、乙、丙三人各自答对这道题的概率,是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
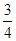 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是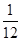 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是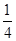 .
.