题目内容
设  在
在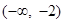 和
和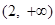 上是单调增函数;
上是单调增函数;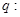 不等式
不等式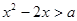 的解集为
的解集为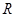 。如果
。如果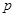 与
与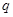 有且只有一个正确,求
有且只有一个正确,求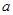 的取值范围。
的取值范围。
 在
在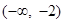 和
和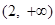 上是单调增函数;
上是单调增函数;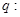 不等式
不等式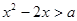 的解集为
的解集为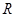 。如果
。如果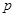 与
与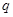 有且只有一个正确,求
有且只有一个正确,求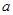 的取值范围。
的取值范围。命题p:由原式得f(x)=x3-ax2-4x+4a,∴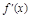 =3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.由条件得
=3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.由条件得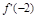 ≥0且
≥0且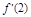 ≥0,即
≥0,即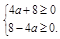 ∴-2≤a≤2.
∴-2≤a≤2.
命题q: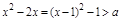 ∵该不等式的解集为R,∴a<-1.当p正确q不正确时,-1≤a≤2;当p不正确q正确时,a<-2.∴a的取值范围是(-∞,-2)∪[-1,2].
∵该不等式的解集为R,∴a<-1.当p正确q不正确时,-1≤a≤2;当p不正确q正确时,a<-2.∴a的取值范围是(-∞,-2)∪[-1,2].
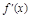 =3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.由条件得
=3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.由条件得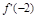 ≥0且
≥0且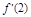 ≥0,即
≥0,即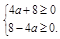 ∴-2≤a≤2.
∴-2≤a≤2.命题q:
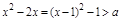 ∵该不等式的解集为R,∴a<-1.当p正确q不正确时,-1≤a≤2;当p不正确q正确时,a<-2.∴a的取值范围是(-∞,-2)∪[-1,2].
∵该不等式的解集为R,∴a<-1.当p正确q不正确时,-1≤a≤2;当p不正确q正确时,a<-2.∴a的取值范围是(-∞,-2)∪[-1,2].略

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
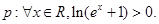 则
则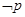 为
为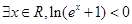
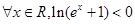
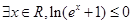
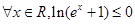
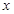 的不等式
的不等式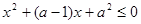 的解集为
的解集为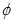 ;
;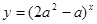 为增函数.
为增函数.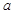 的取值范围.
的取值范围.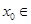 R,
R,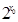
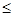 0”的否定是( ).
0”的否定是( ). 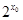 >0
>0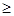 0
0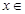 R,
R, 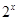
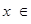 R,
R, 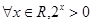
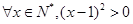
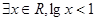
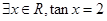
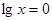 ,则
,则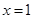 ”的逆否命题为“若
”的逆否命题为“若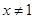 ,则
,则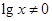 ”
” 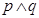 为假命题,则
为假命题,则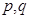 均为假命题
均为假命题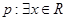 ,使得
,使得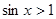 ,则
,则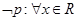 ,均有
,均有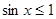
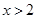 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件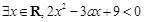 ”为假命题,则实数
”为假命题,则实数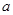 的取值范围是
的取值范围是 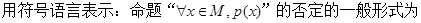
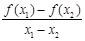 >0.则给出下列命题:
>0.则给出下列命题: