题目内容
设函数g(x)=x2-2(x∈R),f(x)=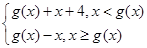 则f(x)的值域是( )
则f(x)的值域是( )
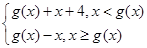 则f(x)的值域是( )
则f(x)的值域是( )A.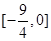 ∪(1,+∞) ∪(1,+∞) |
| B.[0,+∞) |
C.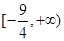 |
D.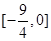 ∪(2,+∞) ∪(2,+∞) |
D
令x<g(x),即x2-x-2>0,
解得x<-1或x>2.
令x≥g(x),即x2-x-2≤0,解得-1≤x≤2.
故函数f(x)=
当x<-1或x>2时,函数f(x)>f(-1)=2;
当-1≤x≤2时,函数 ≤f(x)≤f(-1),
≤f(x)≤f(-1),
即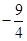 ≤f(x)≤0.
≤f(x)≤0.
故函数f(x)的值域是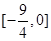 ∪(2,+∞).选D.
∪(2,+∞).选D.
解得x<-1或x>2.
令x≥g(x),即x2-x-2≤0,解得-1≤x≤2.
故函数f(x)=

当x<-1或x>2时,函数f(x)>f(-1)=2;
当-1≤x≤2时,函数
 ≤f(x)≤f(-1),
≤f(x)≤f(-1),即
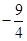 ≤f(x)≤0.
≤f(x)≤0.故函数f(x)的值域是
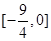 ∪(2,+∞).选D.
∪(2,+∞).选D.
练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
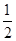 ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0,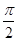 ]上的值域为( )
]上的值域为( )
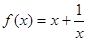 (
(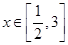 ),则函数
),则函数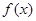 的值域为
的值域为 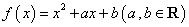 的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )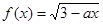 在区间
在区间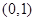 是减函数,则实数
是减函数,则实数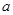 的取值范围是 .
的取值范围是 .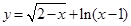 的定义域为 .
的定义域为 .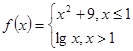 ,记
,记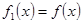 ,
,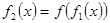 ,
,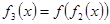 ,
,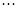 ,则
,则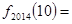 ( )
( )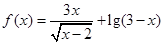 的定义域是( )
的定义域是( )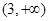
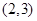
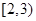
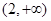
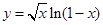 的定义域为( )
的定义域为( )