题目内容

设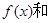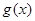是定义在R上的两个函数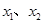，是R上任意两个不等的实根，设

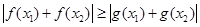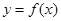恒成立，且为奇函数，判断函数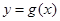的奇偶性并说明理由。

 

【答案】

函数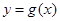为奇函数，见解析。

【解析】本试题主要是考查了函数的奇偶性的证明。

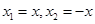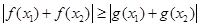先分析令，所以即为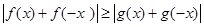

又由已知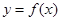为奇函数，故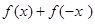＝0

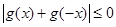所以，可知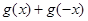＝0对任意的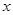都成立得到结论。

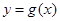证明：函数为奇函数

以下证明：令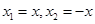，………………………………….1分

所以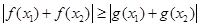即为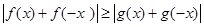。。。。。。。2分

又由已知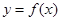为奇函数，故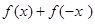＝0

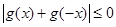所以，可知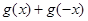＝0对任意的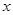都成立，。。。。。。。。。。。4分

又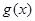是定义在R上的函数，定义域关于原点对称    ∴函数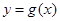为奇函数。。。。6分

 

练习册系列答案
相关题目
设f（x）和g（x）是定义在R上的两个函数，x1、x2是R上任意两个不等的实根，设|f（x1）+f（x2）|≥|g（x1）+g（x2）|恒成立，且y=f（x）为奇函数，判断函数y=g（x）的奇偶性并说明理由．
（2012•安徽模拟）给出以下命题：
①函数f(x)=|log2x2|既无最大值也无最小值；
②函数f（x）=|x2-2x-3|的图象关于直线x=1对称；
③若函数f（x）的定义域为（0，1），则函数f（x2）的定义域为（-1，1）；
④若函数f（x）满足|f（-x）|=|f（x）|，则函数f（x）或是奇函数或是偶函数；
⑤设f（x）与g（x）是定义在R上的两个函数，若对任意x1，x2∈R（x1≠x2）有|f（x1）-f（x2）|＞|g（x1）-g（x2）|恒成立，且函数f（x）在R上递增，则函数h（x）=f（x）-g（x）在R上递增．
其中正确的命题是
②④⑤
②④⑤
（写出所有真命题的序号）
给出以下命题：
①函数f(x)=|log2x2|既无最大值也无最小值；
②函数f（x）=|x2-2x-3|的图象关于直线x=1对称；
③若函数f（x）的定义域为（0，1），则函数f（x2）的定义域为（-1，1）；
④若函数f（x）满足|f（-x）|=|f（x）|，则函数f（x）或是奇函数或是偶函数；
⑤设f（x）与g（x）是定义在R上的两个函数，若对任意x1，x2∈R（x1≠x2）有|f（x1）-f（x2）|＞|g（x1）-g（x2）|恒成立，且函数f（x）在R上递增，则函数h（x）=f（x）-g（x）在R上递增．
其中正确的命题是______（写出所有真命题的序号）
给出以下命题：
①函数既无最大值也无最小值；
②函数f（x）=|x2-2x-3|的图象关于直线x=1对称；
③若函数f（x）的定义域为（0，1），则函数f（x2）的定义域为（-1，1）；
④若函数f（x）满足|f（-x）|=|f（x）|，则函数f（x）或是奇函数或是偶函数；
⑤设f（x）与g（x）是定义在R上的两个函数，若对任意x1，x2∈R（x1≠x2）有|f（x1）-f（x2）|＞|g（x1）-g（x2）|恒成立，且函数f（x）在R上递增，则函数h（x）=f（x）-g（x）在R上递增．
其中正确的命题是    （写出所有真命题的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网