题目内容
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a,b∈[-1,1],a+b≠0有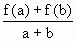 >0恒成立.
>0恒成立.
(Ⅰ)判断f(x)在[-1,1]上是增函数还是减函数,并证明你的结论;
(Ⅱ)解不等式f(x+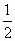 )<f(
)<f(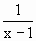 );
);
(Ⅲ)若f(x)≤m2-2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
解析:
|
解(Ⅰ)设x1<x2且x1,x2∈[-1,1],则-x2∈[-1,1] ∵f(x)是奇函数 ∴f(x1)-f(x2)=f(x1)+f(-x2)= 由题设知 ∴ ∴f(x)在[-1,1]上是增函数 (Ⅱ)∵f(x)在[-1,1]上是增函数,不等式等价于 ∴- (Ⅲ)解法一:由(Ⅰ)知,f(x)在[-1,1]上是增函数,且f(1)=1 ∴|f(x)|≤f(1)=1 要f(x)≤m2-2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立 必f(x)max=1≤m2-2am+1成立 ∴必m2-2am≥0 令g(a)=-2am+m2,对a∈[-1,1],g(a)≥0恒成立 只要g(a)最小值大于或等于0 (i)当m<0时,g(a)是增函数,必g(-1)=2m+m2≥0 ∴m≤-2或m≥0,由m<0 ∴m≤-2 (ii)当m=0时,g(a)=0恒成立 (iii)当m>0时,g(a)在[-1,1]上是减函数,必g(1)=-2m+m2≥0 ∴m≤0或m≥2,∵m>0,∴m≥2 综上知,m≤-2或m=0或m≥2 解法二:令g(a)=-2am+m2,对a∈[-1,1],g(a)≥0恒成立 只要g(a)满足 ∴m≤-2或m=0或m≥2 |

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案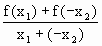 (x1-x2)
(x1-x2)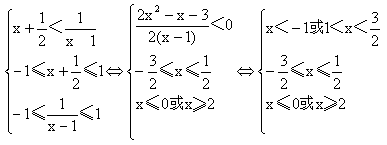
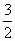 ≤x<-1
≤x<-1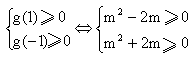
 相等?若存在,求x的值;若不存在,请说明理由.
相等?若存在,求x的值;若不存在,请说明理由. sin2A-cos2B+2
sin2A-cos2B+2 且A、B∈R时,y=f(A、B)的图像通过向量
且A、B∈R时,y=f(A、B)的图像通过向量 的平移得到函数y=2cos2A的图像,求向量
的平移得到函数y=2cos2A的图像,求向量