题目内容
 现有楼房一幢,室内面积共计174m2,拟分割成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2,可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.但用于装修筹款不得超过7800元,且游客能住满客房,设分割大房间为x间,小房间为y间,收益为z元
现有楼房一幢,室内面积共计174m2,拟分割成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2,可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.但用于装修筹款不得超过7800元,且游客能住满客房,设分割大房间为x间,小房间为y间,收益为z元(1)写出目标函数z的表达式;
(2)写出x,y所满足的线性约束条件;
(3)求x,y各为多少时能获得最大收益?最大收益是多少?
分析:(1)根据大房间可住游客5名,每名游客每天住宿费40元;小房间可以住游客3名,每名游客每天住宿费50元,可求目标函数z的表达式;
(2)利用室内面积共计174m2,用于装修筹款不得超过7800元,可得线性约束条件;
(3)作出可行域,明确目标函数的意义,即可求得结论.
(2)利用室内面积共计174m2,用于装修筹款不得超过7800元,可得线性约束条件;
(3)作出可行域,明确目标函数的意义,即可求得结论.
解答: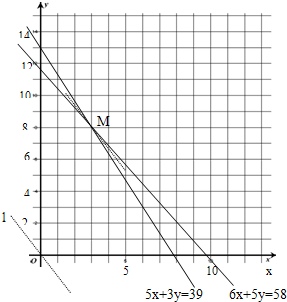 解:设分割大房间为x间,小房间为y间,收益为z元
解:设分割大房间为x间,小房间为y间,收益为z元
根据题意得:
(1)z=200x+150y
(2)
⇒
(3)作出约束条件表示的平面区域
把目标函数z=200x+150y=50(4x+3y)
作直线l:4x+3y=0
平移直线l,直线越往上移,z越大,所以当直线经过M点时,z的值最大,
解方程组
得M(3,8),
最优解是整数解,当直线过M(3,8)时z最大,
∴当x=3,y=8时,z max=1800
 解:设分割大房间为x间,小房间为y间,收益为z元
解:设分割大房间为x间,小房间为y间,收益为z元根据题意得:
(1)z=200x+150y
(2)
|
|
(3)作出约束条件表示的平面区域
把目标函数z=200x+150y=50(4x+3y)
作直线l:4x+3y=0
平移直线l,直线越往上移,z越大,所以当直线经过M点时,z的值最大,
解方程组
|
最优解是整数解,当直线过M(3,8)时z最大,
∴当x=3,y=8时,z max=1800
点评:本题考查线性规划知识,考查目标函数,线性约束条件的确定,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目