Question

某人有楼房一幢，室内面积共180m²，拟分隔成两类房间作为旅游客房．大房间每间面积为18m²，可住游客5名，每名游客每天住宿费为40元；小房间每间面积为15m²，可住游客3名，每名游客每天住宿费为50元；装修大房间每间需1000元，装修小房间每间需600元．如果他只能筹款8000元用于装修，且游客能住满客房，他应隔出大房间和小房间各多少间，能获得最大收益？最大收益是多少？

Answer 1

设隔出大、小房间分别为x间、y间，
收益为Z元则Z=200x+150y，其中x、y满足

18x+15y≤180 1000x+600y≤8000 x∈N，y∈N

，
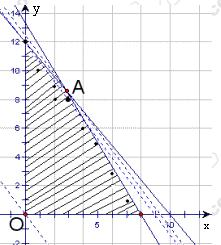
如图所示，
由图解法易得Z=200x+150y过点A（20/7，60/7）时，目标函数Z取得最大值．
但x、y必须是整数，还需在可行区域内找出使目标函数Z取得最大值的整点．显然目标函数Z取得最大值的整点一定是分布在可行区域的右上侧，则利用枚举法即可求出整点最优解．
这些整点有：（0，12），（1，10），（2，9），（3，8），（4，6），（5，5），（6，3），（7，1），（8，0），分别代入Z=200x+150y，逐一验证，可得取整点（0，12）或（3，8）时，
Z_max=200×0+150×12=200×3+150×8=1800（元）．
所以要获得最大收益，有两种方案：只隔出小房间12间；或隔出大房间3间，小房间8间．
答：只隔出小房间12间；或隔出大房间3间，小房间8间，能获得最大收益，最大收益是1800元．