题目内容
等比数列{an}的首项a1=-1,前n项和为Sn,若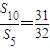 ,则公比q等于 .
,则公比q等于 .
【答案】分析:利用数列前n项和的定义及等比数列通项公式 得出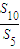 =1+q5=
=1+q5=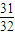 ,解出q即可.
,解出q即可.
解答:解:∵{an}是等比数列,由数列前n项和的定义及等比数列通项公式得S10=(a1+a2+…a5)+(a6+a7+…+a10)=S5+q5(a1+a2+…a5)=(1+q5)S5
∴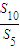 =1+q5=
=1+q5=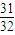 ,q5=
,q5=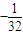 ,q=
,q=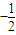 ,
,
故答案为: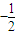 .
.
点评:本题主要考查等比数列前n项和的计算、通项公式.利用数列前n项 定义,避免了在转化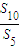 时对公比q是否为1的讨论.
时对公比q是否为1的讨论.
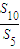 =1+q5=
=1+q5=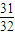 ,解出q即可.
,解出q即可.解答:解:∵{an}是等比数列,由数列前n项和的定义及等比数列通项公式得S10=(a1+a2+…a5)+(a6+a7+…+a10)=S5+q5(a1+a2+…a5)=(1+q5)S5
∴
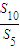 =1+q5=
=1+q5=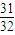 ,q5=
,q5=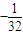 ,q=
,q=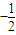 ,
,故答案为:
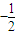 .
.点评:本题主要考查等比数列前n项和的计算、通项公式.利用数列前n项 定义,避免了在转化
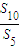 时对公比q是否为1的讨论.
时对公比q是否为1的讨论. 
练习册系列答案
相关题目