题目内容
已知A、B为x轴上不同的两点，点P的横坐标为1，且|PA|=|PB|，若直线PA的方程为x-y+1=0，则直线PB的方程为 （ ）A．x+y-3=0
B．x+3y-7=0
C．x+y-5=0
D．2y-x-3=0
【答案】分析：利用直线PA的方程为x-y+1=0求出PA的斜率，根据|PA|=|PB|，求出PB的倾斜角，再求出P的坐标，然后可求出直线PB的方程．
解答：解：由于直线PA的方程为x-y+1=0，∴直线PA的倾斜角为45°，
∵|PA|=|PB|，∴直线PB的倾斜角为135°，
又当x=1时，y=2，即P（1，2），
∴直线PB的方程为y-2=-（x-1），即x+y-3=0．
故选A
点评：本题考查与直线关于点、直线对称的直线方程，考查逻辑推理能力，计算能力，转化思想的应用，是基础题．
解答：解：由于直线PA的方程为x-y+1=0，∴直线PA的倾斜角为45°，
∵|PA|=|PB|，∴直线PB的倾斜角为135°，
又当x=1时，y=2，即P（1，2），
∴直线PB的方程为y-2=-（x-1），即x+y-3=0．
故选A
点评：本题考查与直线关于点、直线对称的直线方程，考查逻辑推理能力，计算能力，转化思想的应用，是基础题．
练习册系列答案
相关题目
已知F是椭圆
已知A、B为椭圆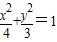
的左右顶点，F为椭圆的右焦点，P是椭圆上异于A、B的任意一点，直线AP、BP分别交直线l：x=m（m＞2）于M、N两点，l交x轴于C点．