题目内容
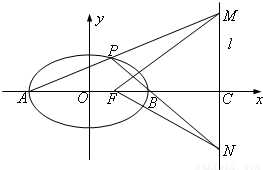
已知A、B为椭圆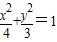 的左右顶点,F为椭圆的右焦点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
的左右顶点,F为椭圆的右焦点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.(Ⅰ)当PF∥l时,求直线AM的方程;
(Ⅱ)是否存在实数m,使得以MN为直径的圆过点F,若存在,求出实数m的值;,若不存在,请说明理由;
(Ⅲ)对任意给定的m值,求△MFN面积的最小值.
【答案】分析:(Ⅰ)由椭圆方程求出F点的坐标,由PF∥l求出P点坐标,直接利用两点式写出直线AM的方程;
(Ⅱ)设出点P、M、N的坐标,由MF和NF垂直得到M和N点坐标的关系,再由A、P、M和B、P、N分别共线得到M的坐标与P的坐标及N的坐标与P的坐标的关系式,三个关系式整理后得到矛盾的式子,说明不存在实数m,使得以MN为直径的圆过点F;
(Ⅲ)结合(Ⅱ),把|MN|用含有P点的坐标表示,得到的几何意义是|MN|是直线CP斜率绝对值的倒数的3倍,当CP与椭圆相切时斜率的绝对值最大,倒数最小,此时面积最小,然后设出过C且与椭圆相切的直线方程,由判别式等于0得到直线斜率k与m的关系,把P点的坐标用m表示,得到|MN|,则三角形MFN面积的最小值可求.
解答:解:(Ⅰ)当PF平行于L时,PF垂直于x轴,则A(-2,0),P(1, ),
),
又因为A、P、M共线,所以用A、P两点坐标求得直线AM的方程为: .
.
即x-2y+2=0;
(Ⅱ)设存在,设P(x,y),M(m,y1),N(m,y2).
由MF垂直于NF可得(m-1)2+y1y2=0(*)
又由MPA三点共线可以算得: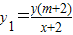 ①
①
由NPB三点共线可得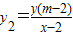 ②
②
将①②两式带入*式可得: .
.
又因为(x,y)在椭圆上,得 ,代入上式化简得m2=-8,此式不成立.
,代入上式化简得m2=-8,此式不成立.
所以不存在实数m,使得以MN为直径的圆过点F;
(Ⅲ)由(Ⅱ)计算得|MN|=|y1-y2|=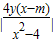
=3| |,其几何意义是直线CP斜率绝对值的倒数的3倍,
|,其几何意义是直线CP斜率绝对值的倒数的3倍,
当CP与椭圆相切时斜率的绝对值最大,倒数最小,此时面积最小,
设过C(m,0)且与椭圆切于P点的直线为y=k(x-m),
联立 ,得(3+4k2)x2-8mk2+4k2m2-12=0.
,得(3+4k2)x2-8mk2+4k2m2-12=0.
由△=(-8mk2)2-4(3+4k2)(4k2m2-12)=0,得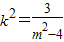 .
.
当直线与椭圆相切时,切点P的横坐标 .
.
纵坐标 .
.
所以|MN|=3|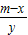 |=
|=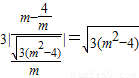 .
.
所以△MFN面积为 .
.
点评:本题考查了直线的一般是方程,考查了三角形的面积公式,考查了直线与圆锥曲线的关系,考查了数形结合的解题思想方法与数学转化思想方法,考查了学生综合处理问题解决问题的能力,考查了学生的运算能力,是难题.
(Ⅱ)设出点P、M、N的坐标,由MF和NF垂直得到M和N点坐标的关系,再由A、P、M和B、P、N分别共线得到M的坐标与P的坐标及N的坐标与P的坐标的关系式,三个关系式整理后得到矛盾的式子,说明不存在实数m,使得以MN为直径的圆过点F;
(Ⅲ)结合(Ⅱ),把|MN|用含有P点的坐标表示,得到的几何意义是|MN|是直线CP斜率绝对值的倒数的3倍,当CP与椭圆相切时斜率的绝对值最大,倒数最小,此时面积最小,然后设出过C且与椭圆相切的直线方程,由判别式等于0得到直线斜率k与m的关系,把P点的坐标用m表示,得到|MN|,则三角形MFN面积的最小值可求.
解答:解:(Ⅰ)当PF平行于L时,PF垂直于x轴,则A(-2,0),P(1,
 ),
),又因为A、P、M共线,所以用A、P两点坐标求得直线AM的方程为:
 .
.即x-2y+2=0;
(Ⅱ)设存在,设P(x,y),M(m,y1),N(m,y2).
由MF垂直于NF可得(m-1)2+y1y2=0(*)
又由MPA三点共线可以算得:
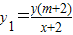 ①
①由NPB三点共线可得
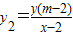 ②
②将①②两式带入*式可得:
 .
.又因为(x,y)在椭圆上,得
 ,代入上式化简得m2=-8,此式不成立.
,代入上式化简得m2=-8,此式不成立.所以不存在实数m,使得以MN为直径的圆过点F;
(Ⅲ)由(Ⅱ)计算得|MN|=|y1-y2|=
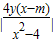
=3|
 |,其几何意义是直线CP斜率绝对值的倒数的3倍,
|,其几何意义是直线CP斜率绝对值的倒数的3倍,当CP与椭圆相切时斜率的绝对值最大,倒数最小,此时面积最小,
设过C(m,0)且与椭圆切于P点的直线为y=k(x-m),
联立
 ,得(3+4k2)x2-8mk2+4k2m2-12=0.
,得(3+4k2)x2-8mk2+4k2m2-12=0.由△=(-8mk2)2-4(3+4k2)(4k2m2-12)=0,得
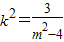 .
.当直线与椭圆相切时,切点P的横坐标
 .
.纵坐标
 .
.所以|MN|=3|
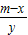 |=
|=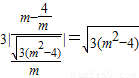 .
.所以△MFN面积为
 .
.点评:本题考查了直线的一般是方程,考查了三角形的面积公式,考查了直线与圆锥曲线的关系,考查了数形结合的解题思想方法与数学转化思想方法,考查了学生综合处理问题解决问题的能力,考查了学生的运算能力,是难题.

练习册系列答案
相关题目
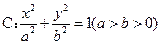 的左,右顶点,
的左,右顶点, ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线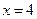 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
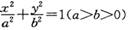 的左、右顶点,C(0,b),直线
的左、右顶点,C(0,b),直线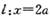 与X轴交于点D,与直线AC交于点P,且BP平分
与X轴交于点D,与直线AC交于点P,且BP平分 ,则此椭圆的离心率为
,则此椭圆的离心率为 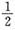 (B)
(B) (C)
(C)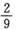 (D)
(D)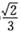
 的左,右顶点,
的左,右顶点,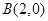 ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线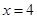 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点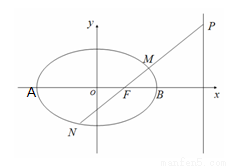

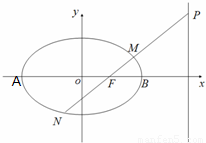 已知A,B是椭圆
已知A,B是椭圆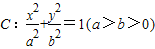 的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点