题目内容
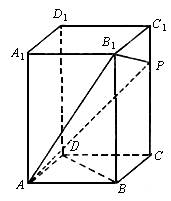
在正四棱柱ABCD—A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的任一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD^AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成二面角的余弦值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是ÐB1AC的平
分线.
答案:
解析:
解析:
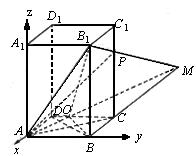
证明:由题意可知,不论P点在棱CC1上的任何位置,AP在底面ABCD内射影都是AC,∵ BD^AC,∴ BE^AP. (2)解:延长B1P和BC,设B1P∩BC=M,连结AM,则AM=平面AB1P∩平面ABCD.过B作BQ^AM于Q,连结B1Q,由于BQ是B1Q在底面ABCD内的射影,所以B1Q^AM,故ÐB1QB就是所求二面角的平面角,依题意,知CM=2B1C1,从而BM=3BC. 所以AM+ BQ= ∴ tanÐB1QB= ∴ cosÐB1QB= (3)解:设CP=a,BC=m,则BB1=2m,C1P=2m-a,从而B1P2=m2+(2m-a)2,
在RtDACP中,cosÐAPC= 依题意,得ÐPAC=ÐPAB1.∴ ∴ AP2+ ∴ 另解:如图,建立空间直角坐标系. 设CP=a,CC1=6,∴ B1(0,3,6),C(-3,3,0),P(-3,3,a). ∴
依题意,得 即 3+2a= 故P距C点的距离是侧棱的
|

练习册系列答案
相关题目
 ,
,

 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点. 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.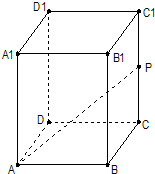 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)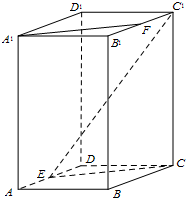 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.