题目内容
在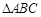 中,内角
中,内角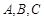 的对边分别为
的对边分别为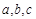 ,且
,且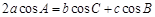 .
.
(1)求角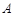 的大小;
的大小;
(2)若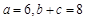 ,求
,求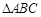 的面积.
的面积.
(1)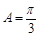 ;(2)
;(2)
解析试题分析:(1)三角形中的化简问题,涉及边角混合的方程,往往需要利用正弦定理或余弦定理进行边角转化,该题中利用正弦定理将边转化为角,得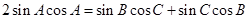 ,即
,即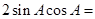
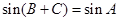 ,
,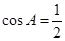 ,进而求A;(2)由(1)得
,进而求A;(2)由(1)得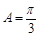 ,联系结论,不难想到
,联系结论,不难想到 ,故求
,故求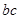 成为解题关键,由余弦定理,得
成为解题关键,由余弦定理,得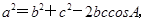 及
及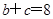 ,求得
,求得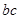 ,进而求
,进而求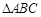 的面积.
的面积.
试题解析:(1)由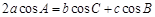 及余弦定理或正弦定理可得
及余弦定理或正弦定理可得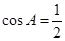
所以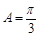
(2)由余弦定理a2=b2+c2-2bccosA,得b2+c2-bc=36.又b+c=8,所以bc=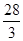 .
.
由三角形面积公式S= bcsinA,得△ABC的面积为
bcsinA,得△ABC的面积为 .
.
考点:1、正弦定理;2、两角和的三角函数;3、余弦定理.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 ,且
,且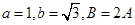 。
。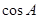 的值;(2)求c的值。
的值;(2)求c的值。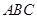 中,角
中,角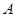 、
、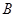 、
、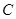 所对的边长分别为
所对的边长分别为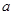 、
、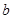 、
、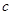 ,
,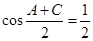 .
. ,
,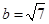 ,求
,求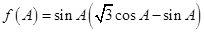 ,求
,求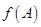 的取值范围.
的取值范围. 中,角
中,角 的对边分别为
的对边分别为 ,且
,且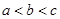 ,
, .
. 的大小;
的大小;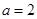 ,
,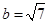 ,求
,求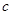 边的长和△
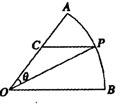
边的长和△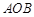 ,圆心角
,圆心角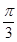 ,半径为2,在半径
,半径为2,在半径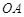 上有一动点
上有一动点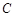 ,过点
,过点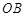 的直线交弧
的直线交弧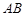 于点
于点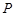 .
.
 的长;
的长; ,求
,求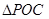 面积的最大值及此时
面积的最大值及此时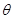 的值.
的值. .
.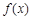 的最小正周期和值域;
的最小正周期和值域;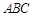 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
,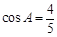 ,求
,求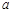 和
和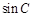 .
.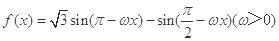 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
. 的值;
的值; 中,
中,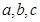 分别是角
分别是角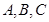 的对边,且
的对边,且 ,求
,求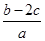 的取值范围.
的取值范围. ,a=5,△ABC的面积为10
,a=5,△ABC的面积为10
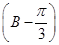 的值.
的值.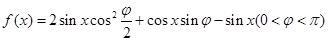 在
在 处取最小值.
处取最小值. 的值。
的值。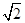 ,
,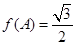 ,求角C.
,求角C.