题目内容
4．已知函数f（x）=$\left\{\begin{array}{l}{（-x）^{\frac{1}{2}}}，x≤0\\{log_2}x，x＞0\end{array}$，函数g（x）是周期为2的偶函数且当x∈[0，1]时，g（x）=2x-1，则函数y=f（x）-g（x）的零点个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 画出函数f（x）和函数g（x）的图象，数形结合，可得答案．
解答 解：画出函数f（x）和函数g（x）的图象，如下图所示：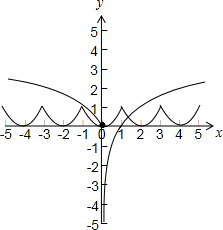
由图可得：两个函数图象共有3个交点，
故函数y=f（x）-g（x）有3个零点，
故选：C．
点评 本题考查的知识点是分段函数的应用，函数的周期性，指数函数的图象和性质，函数图象的平移变换，函数的零点，是函数图象和性质的综合应用，难度中档．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表如下：
（1）根据样本估计这批苹果的平均重量；
（2）根据样本估计这批苹果重量的中位数；
（3）用分层抽样的方法从重量在[80，85）和[95，100）的苹果中共抽取8个，其中重量在[80，85）的有几个？
| 分组（重量） | [80，85） | [85，90） | [90，95） | [95，100） |
| 频数（个） | 5 | 10 | 20 | 15 |
（2）根据样本估计这批苹果重量的中位数；
（3）用分层抽样的方法从重量在[80，85）和[95，100）的苹果中共抽取8个，其中重量在[80，85）的有几个？
4．$\sqrt{{9}^{\frac{3}{2}}}$的值为（ ）
| A． | $\sqrt{3}$ | B． | 3$\sqrt{3}$ | C． | 3 | D． | 729 |
9．连续抛掷骰子，记下每次面朝上的点数，若出现三个不同的数就停止，问抛掷5次停止时，会出现不同的结果种数位 （ ）
| A． | 420 | B． | 840 | C． | 720 | D． | 640 |
16．随着城市车辆的增加，城市的空气污染越来越严重，空气质量指数API一直居高不下，对人体的呼吸系统造成了严重的影响．现调查了某市500名居民的工作场所和呼吸系统健康，得到2×2列联表如下
补全2×2列联表，并回答能否有99%的把握认为“感染呼吸系统疾病和工作场所有关”．
参考公式：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$．
| 室外工作 | 室内工作 | 合计 | |
| 有呼吸系统疾病 | 150 | ||
| 无呼吸系统疾病 | 110 | ||
| 合计 | 200 |
| P（Χ2≥k） | 0.050 0.025 0.010 |
| k | 3.841 5.024 6.635 |