题目内容
15.盒中有5值LED节能灯,其中有2只是坏的,现从盒中随机地抽取2只,那么$\frac{3}{5}$是( )| A. | 2只全是坏的概率 | B. | 2中全是好的概率 | ||
| C. | 恰有1只是坏的概率 | D. | 至少1只是坏的概率 |
分析 把从5只LED节能灯随机地抽取2只情况分类,求出每一类的概率,由对立事件的概率可得答案.
解答 解:从5只LED节能灯中随机地抽取2只,情况有三种,两只都是好的,两只都是坏的,一只好的和一只坏的.
两只都是好的概率为P1=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$;两只都是坏的概率为P2=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$;
一只好的一只坏的概率为P3=$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}$=$\frac{6}{10}$=$\frac{3}{5}$.
故选:C.
点评 本题考查了古典概型及其概率计算公式,考查了互斥事件和对立事件的概率,是基础题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
5.向量$\overrightarrow a=(-2,1)$,$\overrightarrow b=(λ,1)$,若$\vec a$与$\vec b$的夹角为钝角,则λ的范围( )
| A. | $(\frac{1}{2},2)∪(2,+∞)$ | B. | (2,+∞) | C. | $(-∞,-\frac{1}{2})$ | D. | $(\frac{1}{2},+∞)$ |
10.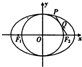 如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
 如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
7.若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=x2+3x+1,则f(x)=( )
| A. | x2 | B. | 2x2 | C. | 2x2+2 | D. | x2+1 |
5.设集合Sn={1,2,3,…,n},若Z是Sn的子集,把Z中的所有数的和称为Z的“容量”(规定空集的容量为0).若Z的容量为奇(偶)数,则称Z为Sn的奇(偶)子集.
命题①:Sn的奇子集与偶子集个数相等;
命题②:当n≥3时,Sn的所有奇子集的容量之和与所有偶子集的容量之和相等
则下列说法正确的是( )
命题①:Sn的奇子集与偶子集个数相等;
命题②:当n≥3时,Sn的所有奇子集的容量之和与所有偶子集的容量之和相等
则下列说法正确的是( )
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
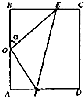 某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)