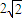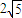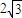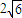题目内容
平面上当两坐标轴不垂直时,称为斜坐标系.斜坐标定义为:若
=x0•
+y0•
(其中
,
分别是斜坐标系的x轴,y轴的单位向量),则称点P的坐标为(x0,y0).在平面斜坐标系∠xoy=60°中,两点A(1,2),B(3,4)的距离为( )
| OP |
| i |
| j |
| i |
| j |
分析:由斜坐标定义得到向量
、
关于x轴,y轴的单位向量
,
的线性表示式,再用向量的减法法则得到向量
=2
+2
.最后利用向量数量积的运算性质,计算出|
|2,代入题中单位向量的长度与
,
数量积的数据,可得A、B两点的距离为2
.
| OA |
| OB |
| i |
| j |
| AB |
| i |
| j |
| AB |
| i |
| j |
| 3 |
解答: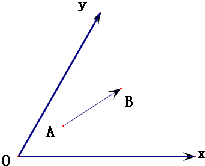 解:∵A的坐标为(1,2),B的坐标为(3,4),
解:∵A的坐标为(1,2),B的坐标为(3,4),
∴
=
+2
,
=3
+4
所以向量
=
-
=2
+2
∵∠xoy=60°,
,
分别是斜坐标系的x轴,y轴的单位向量
∴|
|=|
| =1,
•
=|
|•|
| cos60°=
因此|
|2=(2
+2
)2=4|
|2+8
•
+4|
|2
=4×12+8×
+4×12=12
∴|
| =
=2
,即A、B两点的距离为2
故选C
 解:∵A的坐标为(1,2),B的坐标为(3,4),
解:∵A的坐标为(1,2),B的坐标为(3,4),∴
| OA |
| i |
| j |
| OB |
| i |
| j |
所以向量
| AB |
| OB |
| OA |
| i |
| j |
∵∠xoy=60°,
| i |
| j |
∴|
| i |
| j |
| i |
| j |
| i |
| j |
| 1 |
| 2 |
因此|
| AB |
| i |
| j |
| i |
| i |
| j |
| j |
=4×12+8×
| 1 |
| 2 |
∴|
| AB |
| 12 |
| 3 |
| 3 |
故选C
点评:本题以斜坐标系为例,考查了向量的线性运算和向量数量积的公式,并且考查了利用向量的长度公式求两点之间的距离,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
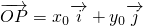 (其中
(其中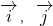 分别是斜坐标系的x轴,y轴的单位向量),则称点P的坐标为(x0,y0).在平面斜坐标系∠xoy=60°中,两点A(1,2),B(3,4)的距离为
分别是斜坐标系的x轴,y轴的单位向量),则称点P的坐标为(x0,y0).在平面斜坐标系∠xoy=60°中,两点A(1,2),B(3,4)的距离为



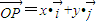 (其中
(其中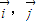 分别是斜坐标系的x轴,y轴的单位向量),则称点P的坐标为(x,y).在平面斜坐标系∠xoy=60°中,两点A(1,2),B(3,4)的距离为( )
分别是斜坐标系的x轴,y轴的单位向量),则称点P的坐标为(x,y).在平面斜坐标系∠xoy=60°中,两点A(1,2),B(3,4)的距离为( )