题目内容
下列四个命题中：①
；②
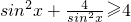；③设x，y都是正数，若
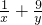=1，则x+y的最小值是12；④若|x-2|＜ε，|y-2|＜ε，则|x-y|＜2ε，则其中所有真命题的个数有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析：使用基本不等式时，要注意“一正，二定，三相等”，否则就不成立．另外注意使用含绝对值不等式性质的应用．
解答：①只有当a，b≥0，才成立，否则不成立；
②由基本不等式得：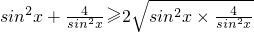
=4，当且仅当sin2x=2取等号，但是six2x=2无解，故
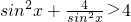，因此②成立．
③x+y=（x+y）×1=（x+y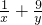）×（）=1+9+
≥10+2
=10+2×3=16，当且仅当
时取等号，故（x+y）min=16，因此③不成立．
④由含绝对值不等式的性质可得：|x-y|=|（x-?）-（y-?）|≤|x-?|+|y-?|＜?+?=2?，故④成立．
综上可知：只有②④是真命题．
故选B．
点评：本题考查了基本不等式及含绝对值不等式性质的应用，熟练掌握以上知识（特别是等号成立的条件）是解决问题的关键．
分析：使用基本不等式时，要注意“一正，二定，三相等”，否则就不成立．另外注意使用含绝对值不等式性质的应用．
解答：①只有当a，b≥0，
才成立，否则不成立；②由基本不等式得：
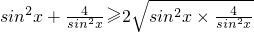=4，当且仅当sin2x=2取等号，但是six2x=2无解，故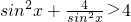，因此②成立．③x+y=（x+y）×1=（x+y）×（
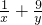）=1+9+≥10+2=10+2×3=16，当且仅当时取等号，故（x+y）min=16，因此③不成立．④由含绝对值不等式的性质可得：|x-y|=|（x-?）-（y-?）|≤|x-?|+|y-?|＜?+?=2?，故④成立．
综上可知：只有②④是真命题．
故选B．
点评：本题考查了基本不等式及含绝对值不等式性质的应用，熟练掌握以上知识（特别是等号成立的条件）是解决问题的关键．
练习册系列答案
相关题目