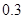题目内容
(本小题12分)为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为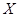 ,求
,求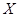 的分布列和数学期望.
的分布列和数学期望.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为
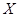 ,求
,求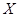 的分布列和数学期望.
的分布列和数学期望.(1)甲、乙两班恰好在前两位出场的概率为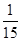 ;(2)分布列:
;(2)分布列:
随机变量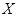 的数学期望为
的数学期望为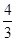
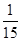 ;(2)分布列:
;(2)分布列: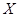 | 0 | 1 | 2 | 3 | 4 |
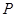 | 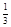 | 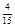 | 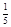 | 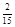 | 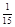 |
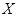 的数学期望为
的数学期望为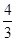
(1)设“甲、乙两班恰好在前两位出场”为事件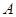 ,则
,则
(2)先确定随机变量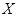 的可能取值为
的可能取值为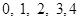 .然后求出每个值对应的概率。列出分布列根据期望公式求解即可。
.然后求出每个值对应的概率。列出分布列根据期望公式求解即可。
解:(1)设“甲、乙两班恰好在前两位出场”为事件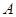 ,则
,则
所以 甲、乙两班恰好在前两位出场的概率为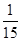 ………………………………4分
………………………………4分
(2)随机变量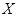 的可能取值为
的可能取值为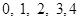 .
.
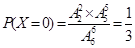 ,
, 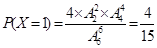 ,
, 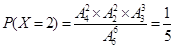 ,
,
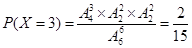
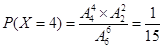 ……………………10分
……………………10分
随机变量 的分布列为:
的分布列为:
因此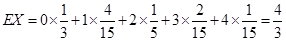 ,
,
即随机变量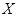 的数学期望为
的数学期望为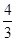 . …………………………12分
. …………………………12分
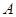 ,则
,则
(2)先确定随机变量
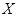 的可能取值为
的可能取值为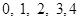 .然后求出每个值对应的概率。列出分布列根据期望公式求解即可。
.然后求出每个值对应的概率。列出分布列根据期望公式求解即可。解:(1)设“甲、乙两班恰好在前两位出场”为事件
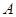 ,则
,则
所以 甲、乙两班恰好在前两位出场的概率为
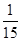 ………………………………4分
………………………………4分(2)随机变量
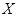 的可能取值为
的可能取值为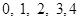 .
. 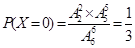 ,
, 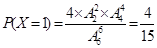 ,
, 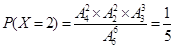 ,
,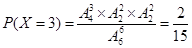
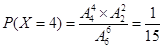 ……………………10分
……………………10分随机变量
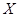 的分布列为:
的分布列为: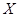 | 0 | 1 | 2 | 3 | 4 |
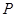 | 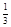 | 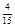 | 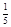 | 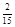 | 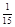 |
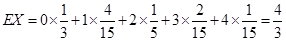 ,
,即随机变量
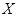 的数学期望为
的数学期望为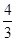 . …………………………12分
. …………………………12分
练习册系列答案
相关题目
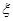 是离散型随机变量,
是离散型随机变量,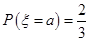 ,
,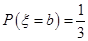 ,且a<b,又Eξ=
,且a<b,又Eξ=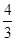 ,Dξ=
,Dξ=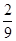 ,则a+b的值为( )
,则a+b的值为( )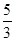


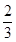 ,被乙小组攻克的概率为
,被乙小组攻克的概率为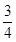 ,
,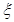 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求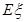 ;
;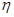 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数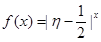 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率; 中任选出两位同学,共同帮助成绩在
中任选出两位同学,共同帮助成绩在 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若 同学成绩为43分,
同学成绩为43分, 同学成绩为95分,求
同学成绩为95分,求 0.785,汽车的碳排放量(千克)=油耗公升数
0.785,汽车的碳排放量(千克)=油耗公升数
 表示25个人中低碳族人数,求E
表示25个人中低碳族人数,求E ):
):
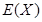 =_______,方差
=_______,方差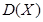 =____________.
=____________. 的分布列如下表所示,
的分布列如下表所示, ,则
,则 的值等于 ;
的值等于 ; 
 的分布如图所示则数学期望
的分布如图所示则数学期望 .
.