题目内容
若Cn1+3Cn2+32Cn3+…+3n-2Cnn-1+3n-1=85,则 n的值为 .
【答案】分析:由题意可得 1+Cn1+3Cn2+32Cn3+…+3n-2Cnn-1+3n-1=86,故 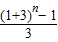 =85,解方程求得n的值.
=85,解方程求得n的值.
解答:解:由题意可得 1+Cn1+3Cn2+32Cn3+…+3n-2Cnn-1+3n-1=86,∴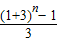 =85,
=85,
∴4n=256,∴n=4,
故答案为:4.
点评:本题考查组合数公式,二项式定理,得到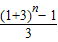 =85,是解题的关键.
=85,是解题的关键.
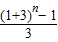 =85,解方程求得n的值.
=85,解方程求得n的值.解答:解:由题意可得 1+Cn1+3Cn2+32Cn3+…+3n-2Cnn-1+3n-1=86,∴
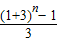 =85,
=85,∴4n=256,∴n=4,
故答案为:4.
点评:本题考查组合数公式,二项式定理,得到
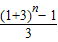 =85,是解题的关键.
=85,是解题的关键. 
练习册系列答案
相关题目