题目内容
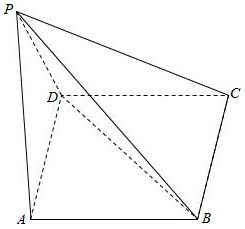
14. 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB,点F是PB的中点,点E在边BC上移动.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB,点F是PB的中点,点E在边BC上移动.(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有PE⊥AF.
分析 (1)当点E为BC的中点时,EF与平面PAC平行;利用中位线性质以及线面平行的判定定理可得;
(2)利用线面垂直的性质定理和判定定理矩形证即可.
解答 解:(1)当点E为BC的中点时,EF与平面PAC平行.…(2分)
理由如下:
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC.
又EF?平面PAC,而PC?平面PAC,
∴EF∥平面PAC.…(6分)
(2)∵PA⊥底面ABCD,BC?平面ABCD,∴PA⊥BC,
又∵ABCD是矩形,∴BC⊥AB.
∵PA∩AB=A,∴BC⊥平面PAB,∵AF?平面PAB,
∴BC⊥AF.…(9分)
PA=AB,点F是PB的中点,∴AF⊥PB.
又∵BC∩PB=B,∴AF⊥平面PBC,∵PE?平面PBC,∴AF⊥PE.
∴无论点E在BC边的何处,都有PE⊥AF.…(12分)
点评 本题实质上考查了线面平行的判定定理的运用以及线面垂直的判定定理和性质定理的运用;熟练运用定理是关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.若BC边上存在两个点Q使得PQ⊥DQ.则a的取值范围是( )
| A. | (1,+∞) | B. | [1,2) | C. | (2,+∞) | D. | [2,4] |
6.曲线f(x)=(2x-m)ex在x=0处的切线与直线x+3y=0垂直,则m等于( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |

 如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.
如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.