题目内容
（理）函数f（x）=x2-ln（2x-1）的单调递减区间是 ．
【答案】分析：求出函数的定义域，求出函数的导数，通过导数小于0，求出x的范围即可．
解答：解：函数f（x）=x2-ln（2x-1）的定义域是{x|x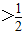
}，
f′（x）=2x-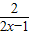
，
令f′（x）＜0，
即2x-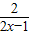
＜0，
∴
，
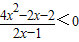即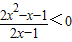
，
∴
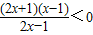，利用穿根法，如图
因为函数f（x）的定义域是{x|x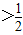
}
所以不等式的解为：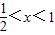
，
所以函数f（x）=x2-ln（2x-1）的单调减区间为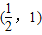
．
故答案为：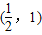
．
点评：本题考查函数的对数求解函数的单调减区间的方法，函数的定义域是易错点，易因为忘记求定义域导致错误，考查计算能力．
解答：解：函数f（x）=x2-ln（2x-1）的定义域是{x|x
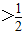}，f′（x）=2x-
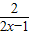，令f′（x）＜0，
即2x-
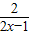＜0，∴
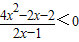，即
，∴
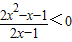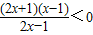，利用穿根法，如图因为函数f（x）的定义域是{x|x
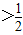}所以不等式的解为：
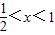，所以函数f（x）=x2-ln（2x-1）的单调减区间为
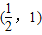．故答案为：
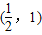．点评：本题考查函数的对数求解函数的单调减区间的方法，函数的定义域是易错点，易因为忘记求定义域导致错误，考查计算能力．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
，|x-2|}，其中min{a，b}=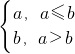
，若动直线y=m与函数y=f（x）f（x）的图象有三个不同的交点，它们的横坐标分别为x1，x2，x3，则x1•x2•x3是否存在最大值？若存在，在横线处填写其最大值；若不存在，直接填写“不存在”________．