题目内容
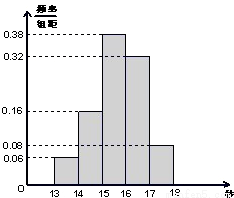 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图.(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)设m,n表示该班某两位同学的百米测试成绩,且已知m,n∈[13,14)∪[17,18],求事件“|m-n|>1”的概率.
【答案】分析:(1)利用频率分布直方图中的频率等于纵坐标乘以组距求出绩大于或等于14秒且小于16秒的频率;利用频数等于频率乘以样本容量求出该班在这次百米测试中成绩良好的人数.
(2)按照(1)的方法求出成绩在[13,14)及在[17,18]的人数;通过列举得到m,n都在[13,14)间或都在[17,18]间或一个在[13,14)间一个在[17,18]间的方法数,三种情况的和为总基本事件的个数;分布在两段的情况数是事件“|m-n|>1”包含的基本事件数;利用古典概型的概率公式求出事件“|m-n|>1”的概率.
解答:解:(1)由直方图知,成绩在[14,16)内的人数为:50×0.16+50×0.38=27(人),
所以该班成绩良好的人数为27人、
(2)由直方图知,成绩在[13,14)的人数为50×0.06=3人,
设为为x,y,z;成绩在[17,18]的人数为50×0,08=4人,设为A、B、C、D.
若m,n∈[13,14)时,有xy,xz,yz共3种情况;
若m,n∈[17,18]时,有AB,AC,AD,BC,BD,CD,共6种情况;
若m,n分别在[13,14)和[17,18]内时,
有12种情况、
所以,基本事件总数为3+6+12=21种,事件“|m-n|>1”所包含的基本事件个数有12种、
∴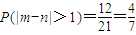 (12分)
(12分)
点评:本题考查频率分布直方图中的频率等于纵坐标乘以组距、考查频数等于频率乘以样本容量、考查列举法求完成事件的方法数、考查古典概型的概率公式.
(2)按照(1)的方法求出成绩在[13,14)及在[17,18]的人数;通过列举得到m,n都在[13,14)间或都在[17,18]间或一个在[13,14)间一个在[17,18]间的方法数,三种情况的和为总基本事件的个数;分布在两段的情况数是事件“|m-n|>1”包含的基本事件数;利用古典概型的概率公式求出事件“|m-n|>1”的概率.
解答:解:(1)由直方图知,成绩在[14,16)内的人数为:50×0.16+50×0.38=27(人),
所以该班成绩良好的人数为27人、
(2)由直方图知,成绩在[13,14)的人数为50×0.06=3人,
设为为x,y,z;成绩在[17,18]的人数为50×0,08=4人,设为A、B、C、D.
若m,n∈[13,14)时,有xy,xz,yz共3种情况;
若m,n∈[17,18]时,有AB,AC,AD,BC,BD,CD,共6种情况;
若m,n分别在[13,14)和[17,18]内时,
| A | B | C | D | |
| x | xA | xB | xC | xD |
| y | yA | yB | yC | yD |
| z | zA | zB | zC | zD |
所以,基本事件总数为3+6+12=21种,事件“|m-n|>1”所包含的基本事件个数有12种、
∴
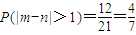 (12分)
(12分)点评:本题考查频率分布直方图中的频率等于纵坐标乘以组距、考查频数等于频率乘以样本容量、考查列举法求完成事件的方法数、考查古典概型的概率公式.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
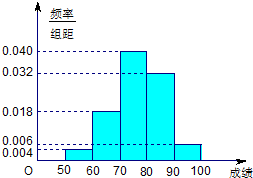 某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.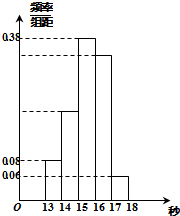 某班50名学生在一次百米测试中,成绩全部在[13,18]内,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15);…第五组[17,18].右图是按上述分组方法得到的频率分布直方图.且第一组,第二组,第四组的频数成等比数列,m,n表示该班某两位同学的百米测试成绩,且m,n∈[13,14)∪[17,18].则事件“|m-n|>1”的概率为( )
某班50名学生在一次百米测试中,成绩全部在[13,18]内,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15);…第五组[17,18].右图是按上述分组方法得到的频率分布直方图.且第一组,第二组,第四组的频数成等比数列,m,n表示该班某两位同学的百米测试成绩,且m,n∈[13,14)∪[17,18].则事件“|m-n|>1”的概率为( )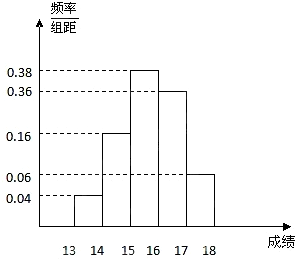 某班50名学生在一次百米测试中,成绩介于13秒与18秒之间.将测试结果分成五组,按上述分组方法得到如下频率分布直方图
某班50名学生在一次百米测试中,成绩介于13秒与18秒之间.将测试结果分成五组,按上述分组方法得到如下频率分布直方图
 某班 50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )
某班 50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )