题目内容
(本题满分12分)、若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,
(1) 求当x∈[1,2]时,f(x)的解析式;
(2) 定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
(1)当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)当t=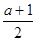 时,S最大值=
时,S最大值=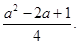
【解析】本试题主要是考查了函数的奇偶性和函数的解析式以及函数的最值的综合运用。
(1)因为∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)利用条件可设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,然后运用坐标表示三角形的面积。
(1)∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2,∴△ABC的面积为S=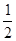 (2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-
(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-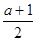 )2+
)2+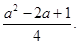
∵2<a<3,∴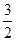 <
<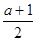 <2.当t=
<2.当t=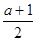 时,S最大值=
时,S最大值=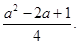

 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面