题目内容
已知向量 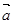 =(1,2) ,
=(1,2) ,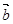 =(cosa,sina),设
=(cosa,sina),设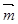 =
=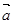 +t
+t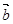 (
(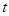 为实数).
为实数).
(1)若a=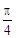 ,求当|
,求当|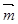 |取最小值时实数
|取最小值时实数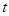 的值;
的值;
(2)若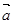 ⊥
⊥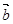 ,问:是否存在实数
,问:是否存在实数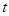 ,使得向量
,使得向量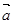 –
–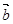 和向量
和向量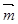 的夹角为
的夹角为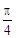 ,若存在,请求出t的值;若不存在,请说明理由.
,若存在,请求出t的值;若不存在,请说明理由.
(3)若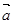 ⊥
⊥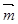 ,求实数
,求实数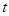 的取值范围A,并判断当
的取值范围A,并判断当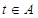 时函数
时函数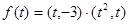 的单调性.
的单调性.
【答案】
解:(1)因为a=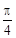 ,
,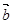 =(
=(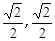 ),
),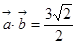 ,…………………2分
,…………………2分
则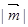 =
=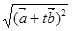 =
=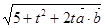 =
=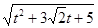 =
=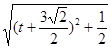
所以当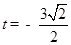 时,
时,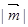 取到最小值,最小值为
取到最小值,最小值为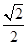 ………………………4分
………………………4分
(2)由条件得cos45 =
=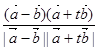 ,………………………5分
,………………………5分
又因为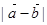 =
=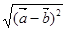 =
=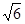 ,
, 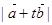 =
=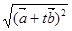 =
=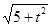 ,
,
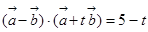 ,………………………………6分
,………………………………6分
则有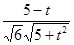 =
=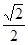 ,且
,且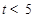 ,
,
整理得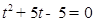 ,所以存在
,所以存在 =
=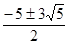 满足条件……………8分
满足条件……………8分
(3) 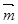 =(1+tcosa,2+tsina)
=(1+tcosa,2+tsina)
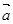 ⊥
⊥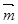
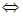 5+t(cosa+2sina)=0
5+t(cosa+2sina)=0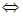
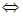 5+
5+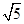 tsin(a+
tsin(a+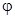 )=0
)=0
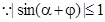
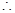
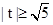
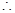
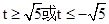 ……………10分
……………10分
又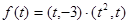 ,
,
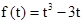
令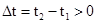 ,则
,则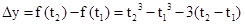
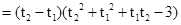
当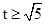 时,
时,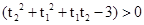 ,
,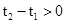
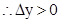
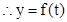 在
在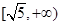 上单调递增
上单调递增
当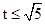 时,
时,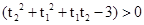 ,
,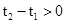
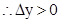
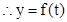 在
在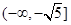 上单调递增…………………………12
上单调递增…………………………12
【解析】略

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目