题目内容
求证:tan2θ(1+cos2θ)=1-cos2θ.
证明:∵等式左边=tan2θ(1+cos2θ)
=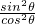 (1+2cos2θ-1)
(1+2cos2θ-1)
=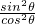 •2cos2θ
•2cos2θ
=2sin2θ,
等式右边=1-cos2θ=1-(1-2sin2θ)=2sin2θ,
∴左边=右边,
故原式成立.
分析:原式的左边括号外边利用同角三角函数间的基本关系把tanθ化为 ,括号里边利用二倍角的余弦函数公式化简,合并后约分即可得到结果;原式的右边利用二倍角的余弦函数公式化简,合并后得到结果,由左边=右边得证.
,括号里边利用二倍角的余弦函数公式化简,合并后约分即可得到结果;原式的右边利用二倍角的余弦函数公式化简,合并后得到结果,由左边=右边得证.
点评:此题考查了三角函数恒等式的证明,用到的知识有同角三角函数间的基本关系,以及二倍角的余弦函数公式,熟练掌握三角函数的恒等变换公式是证明的关键.
=
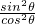 (1+2cos2θ-1)
(1+2cos2θ-1)=
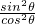 •2cos2θ
•2cos2θ=2sin2θ,
等式右边=1-cos2θ=1-(1-2sin2θ)=2sin2θ,
∴左边=右边,
故原式成立.
分析:原式的左边括号外边利用同角三角函数间的基本关系把tanθ化为
 ,括号里边利用二倍角的余弦函数公式化简,合并后约分即可得到结果;原式的右边利用二倍角的余弦函数公式化简,合并后得到结果,由左边=右边得证.
,括号里边利用二倍角的余弦函数公式化简,合并后约分即可得到结果;原式的右边利用二倍角的余弦函数公式化简,合并后得到结果,由左边=右边得证.点评:此题考查了三角函数恒等式的证明,用到的知识有同角三角函数间的基本关系,以及二倍角的余弦函数公式,熟练掌握三角函数的恒等变换公式是证明的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目