题目内容
(2012•淄博二模)已知α,β是两个不同的平面,直线l⊥α,直线m?β,有下面四个命题:
(1)α∥β⇒l⊥m
(2)α⊥β⇒l∥m
(3)l∥m⇒α⊥β
(4)l⊥m⇒α∥β
其中正确命题的个数是( )
(1)α∥β⇒l⊥m
(2)α⊥β⇒l∥m
(3)l∥m⇒α⊥β
(4)l⊥m⇒α∥β
其中正确命题的个数是( )
分析:(1)
⇒l⊥β,又m?β,则l⊥m;(2)
⇒l∥β或l?β,又m?β,则l与m位置关系不确定;
(3)
⇒m⊥α,又m?β,则α⊥β;(4)
⇒m?α或m∥α,又m?β,推不出α∥β.
|
|
(3)
|
|
解答:解:由于α,β是两个不同的平面,(1)∵α∥β,l⊥α,∴l⊥β,又由直线m?β,∴l⊥m,故(1)正确;
(2)∵α⊥β,l⊥α,∴l∥β或l?β,而m?β,则l与m位置关系不确定,故(2)不正确;
(3)∵l∥m,l⊥α,∴m⊥α,又由直线m?β,∴α⊥β,故(3)正确;
(4)∵l⊥m,l⊥α,∴m?α或m∥α,又m?β,则α∥β或α∩β,故(4)不正确;
故答案选 B.
(2)∵α⊥β,l⊥α,∴l∥β或l?β,而m?β,则l与m位置关系不确定,故(2)不正确;
(3)∵l∥m,l⊥α,∴m⊥α,又由直线m?β,∴α⊥β,故(3)正确;
(4)∵l⊥m,l⊥α,∴m?α或m∥α,又m?β,则α∥β或α∩β,故(4)不正确;
故答案选 B.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了线面、线线的平行与垂直的关系,我们可以用空间几何中的定义、定理、公理对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
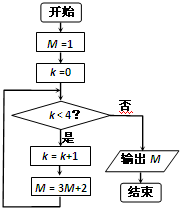 (2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )
(2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )