题目内容
若 ,则函数
,则函数 的两个零点分别位于( )
的两个零点分别位于( )
A. 和 和 内 内 | B. 和 和 内 内 |
C. 和 和 内 内 | D. 和 和 内 内 |
A
解析试题分析:∵a<b<c,∴f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,
由函数零点存在判定定理可知:在区间(a,b),(b,c)内分别存在一个零点;
又函数f(x)是二次函数,最多有两个零点,
因此函数f(x)的两个零点分别位于区间(a,b),(b,c)内.
故选A.
考点:函数零点的判定定理.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A.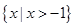 | B.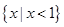 | C. | D. |
对于函数 若
若 则
则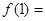 ( )
( )
A.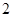 | B. | C. | D. |
函数 的零点所在的区间为( )
的零点所在的区间为( )
A. | B. | C. | D. |
已知集合 ,若
,若 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
方程 有解,则
有解,则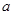 的取值范围( )
的取值范围( )
A. 或 或 | B. |
C. | D. |
已知 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B.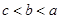 | C. | D. |
 的图象的交点个数为( )
的图象的交点个数为( ) 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象的大致形状是( )
的图象的大致形状是( )
