题目内容
设函数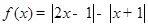 .
.
(1)求不等式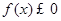 的解集
的解集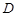 ;
;
(2)若存在实数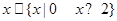 ,使得
,使得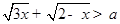 成立,求实数
成立,求实数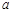 的取值范围.
的取值范围.
(1) ; (2)
; (2)
解析试题分析:(1)由函数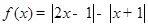 的零点为
的零点为 或
或 .所以将x分为三类即可得到不等式
.所以将x分为三类即可得到不等式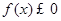 的解集.
的解集.
(2)存在实数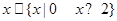 ,使得
,使得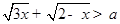 成立,即等价于函数
成立,即等价于函数 的最大值大于
的最大值大于 .由柯西不等式放缩即可求得到
.由柯西不等式放缩即可求得到 的最大值,从而求得实数
的最大值,从而求得实数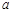 的取值范围,即可得结论.
的取值范围,即可得结论.
(1)当 时,由
时,由 得
得 ,所以
,所以 ;
;
当 时,由
时,由 得
得 ,所以
,所以 ;
;
当 时,由
时,由 得
得 ,所以
,所以 . 2分
. 2分
综上不等式 的解集
的解集
 . 3分
. 3分
(2)
 , 4分
, 4分
由柯西不等式得 ,
, 
 , 5分
, 5分
当且仅当 时取“=”,
时取“=”, 
 的取值范围是
的取值范围是 . 7分
. 7分
考点:1.绝对值不等式.2.柯西不等式.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
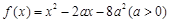 ,记不等式
,记不等式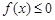 的解集为
的解集为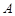 .
.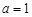 时,求集合
时,求集合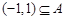 ,求实数
,求实数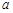 的取值范围.
的取值范围.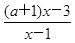 <1.
<1.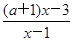 <1.
<1. 若
若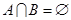 ,求实数
,求实数 的取值范围;
的取值范围;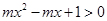 ,对任意实数
,对任意实数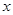 都成立,求
都成立,求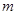 的取值范围.
的取值范围.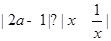 对一切非零实数
对一切非零实数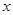 恒成立,则实数
恒成立,则实数 的
的