题目内容
20.以坐标原点为中心,焦点在x轴上的椭圆,长轴长为$2\sqrt{2}$,短轴长为2,过它的左焦点F1作倾斜角为$\frac{π}{3}$的直线l交椭圆于A,B两点,求AB的长.分析 a=$\sqrt{2}$,b=1,可得c=$\sqrt{{a}^{2}-{b}^{2}}$,可得椭圆方程,可得过它的左焦点F1作倾斜角为$\frac{π}{3}$的直线l方程,联立可得关于x的一元二次方程.设A(x1,y1),B(x2,y2),利用|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$即可得出.
解答 解:∵a=$\sqrt{2}$,b=1,∴c=$\sqrt{{a}^{2}-{b}^{2}}$=1.
又∵焦点在x轴上,
∴椭圆方程为$\frac{x^2}{2}+{y^2}=1$,
左焦点F1(-1,0),
∴过它的左焦点F1作倾斜角为$\frac{π}{3}$的直线l方程为$y=\sqrt{3}(x+1)$.
联立$\left\{\begin{array}{l}{y=\sqrt{3}(x+1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为7x2+12x+4=0.
设A(x1,y1),B(x2,y2),
∴$x{\;}_1+{x_2}=-\frac{12}{7}$,$x{\;}_1{x_2}=\frac{4}{7}$,$k=\sqrt{3}$,
从而$|{AB}|=\sqrt{1+{k^2}}|{x{\;}_1-{x_2}}|=\sqrt{(1+{k^2})[{{(x{\;}_1+{x_2})}^2}-4x{\;}_1{x_2}]}=\frac{{8\sqrt{2}}}{7}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.下列分别为集合A到集合B的对应:其中,是从A到B的映射的是( )
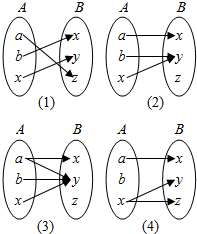

| A. | (1)(2) | B. | (1)(2)( 3) | C. | (1)(2)(4) | D. | (1)(2)(3)(4) |
8.下列命题中的假命题是( )
| A. | ?x∈R,ex>0 | B. | ?x∈R,lnx=0 | C. | ?x∈R,(x-1)2≥0 | D. | ?x∈R,x2+1=0 |
12.若函数f(x)=x2+2(a+1)x+2在(-∞,2)上是减函数,则a的取值范围是( )
| A. | (-∞,-3] | B. | [1,+∞) | C. | [-3,+∞) | D. | (-∞,1] |