题目内容
已知a=(x,0),b=(1,y),(a+(1)求点P(x,y)的轨迹方程;
(2)若直线l:y=kx+m(m≠0)与曲线C交于A、B两点,D(0,-1)且有|![]() |=|
|=|![]() |,试求实数m的取值范围.
|,试求实数m的取值范围.
思路分析:本题是解析几何与平面向量的一道综合题,仔细分析题意并联想到a=(x1,y1),b=(x2,y2).若a·b=0,则a⊥b即可得.
解:(1)由(a+![]() b)⊥(a-
b)⊥(a-![]() b)得a2-3b2=0.
b)得a2-3b2=0.
∴x2-3(1+y2)=0,即![]() -y2=1.
-y2=1.
∴点P(x,y)的轨迹方程为![]() -y2=1.
-y2=1.
(2)由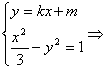 (1-3k2)x2-6kmx-3m2-3=0. ①
(1-3k2)x2-6kmx-3m2-3=0. ①
显然(1-3k2)≠0且Δ=(6km)2-4(1-3k2)(-3m2-3)=12(m2+1-3k2)>0. ②
设x1、x2为方程①的两根,则x1+x2=![]() .
.
∴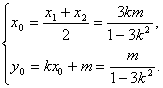
∴AB中点M的坐标为(![]() ).
).
∴线段AB的中垂线的方程为
y-![]() =(-
=(-![]() )(x-
)(x-![]() ).
).
又∵|![]() |=|
|=|![]() |,
|,
∴D(0,-1)是方程的解,代入即得4m=3k2-1,
代入②得12(m2-4m)>0,
即得m<0或m>4.
又∵4m=3k2-1>-1,
∴m>-![]() .
.
故-![]() <m<0或m>4.
<m<0或m>4.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目