题目内容
(08年宝鸡市质检二理) 在直角坐标系![]() 中,已知定点F(1,0)设平面上的动点M在直线
中,已知定点F(1,0)设平面上的动点M在直线![]() 上的射影为N,且满足
上的射影为N,且满足![]() .
.
(1)求动点M的轨迹C的方程;
(2)若直线l是上述轨迹C在点M(顶点除外)处的切线,证明直线MN与l的夹角等于直线ME与l的夹角;
(3)设MF交轨迹C于点Q,直线l交x轴于点P,求△MPQ面积的最小值.
解析:(1)由题意,易知动点![]() 在y轴上及右侧(x≥0).
在y轴上及右侧(x≥0).
且记它在x = -1上的射影为N',∵|MN| =|MF|+1,∴|MN'| = |MF|,∴动点M的轨迹是以F(1,0)为焦点,以直线x = -1为准线的抛物线,![]() .
.
(2)![]() ,设l与MN夹角为
,设l与MN夹角为![]() ,l与M夹角为
,l与M夹角为![]() 由于抛物线C关于x轴对称,不妨设
由于抛物线C关于x轴对称,不妨设![]()
(解法1)当![]() 时,
时,![]() ,从而
,从而![]() ∴直线l的斜率
∴直线l的斜率![]() . 又直线MF的斜率
. 又直线MF的斜率![]() ,
,
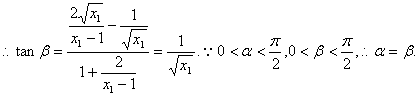
(解法2)设直线l的方程为![]()
将直线方程代入抛物线方程并整理得![]()
![]()
整理得![]()
又![]()
![]()
又由于直线![]() 的斜率
的斜率![]()
![]() . ∴l为∠FMN的平分线.
. ∴l为∠FMN的平分线.
(3)设![]() 则
则![]() .
.
直线l的方程为![]() ,令
,令![]() 得P点坐标
得P点坐标![]()
![]()
![]() ,
,
令![]() 得
得![]() 时,
时,![]()

练习册系列答案
相关题目
