题目内容
长方体三条棱长分别是AA′=1,AB=2,AD=4,则从A点出发,沿长方体的表面到C′的最短矩离是 .
【答案】分析:从A点出发,沿长方体的表面到C′有3条不同的途径,分别从与顶点A相邻的三个面出发,根据勾股定理得到长度分别是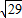 ,
,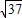 ,5,比较结果,得到结论.
,5,比较结果,得到结论.
解答:解:从A点出发,沿长方体的表面到C′有3条不同的途径,
分别从与顶点A相邻的三个面出发,根据勾股定理得到长度分别是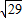 ,
,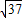 ,5,
,5,
比较三条路径的长度,得到最短的距离是5
故答案为:5.
点评:本题考查多面体和旋转体表面上的最短距离,考查直角三角形的勾股定理,考查分类讨论思想,考查利用几何知识解决实际问题的能力,是一个综合题目,
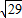 ,
,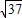 ,5,比较结果,得到结论.
,5,比较结果,得到结论.解答:解:从A点出发,沿长方体的表面到C′有3条不同的途径,
分别从与顶点A相邻的三个面出发,根据勾股定理得到长度分别是
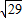 ,
,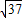 ,5,
,5,比较三条路径的长度,得到最短的距离是5
故答案为:5.
点评:本题考查多面体和旋转体表面上的最短距离,考查直角三角形的勾股定理,考查分类讨论思想,考查利用几何知识解决实际问题的能力,是一个综合题目,

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
长方体三条棱长分别是AA′=1,AB=2,AD=4,则从A点出发,沿长方体的表面到C′的最短矩离是( )
| A、5 | ||
| B、7 | ||
C、
| ||
D、
|