题目内容

5．已知函数y=2x2+5的图象上一点（1，7）及其邻近一点（1+△x，7+△y），则$\frac{△y}{△x}$=4+2△x．

分析 求出f（1+△x），△y=f（1+△x）-f（1），结合定义求解即可．

解答 解：∵f（x）=2x2+5，
∴f（1）=7，
f（1+△x）=2（1+△x）2+5=7+4△x+2（△x）2，
∴△y=4△x+2（△x）2，
即$\frac{△y}{△x}$=$\frac{4△x+2（△x）^{2}}{△x}$=4+2△x，
故答案为：4+2△x．

点评 本题简单的考察变化率的概念，关键是求出自变量的变化量，函数值的变化量，化简求值，属于容易题．

练习册系列答案
相关题目
9．将下列三角函数转化为锐角三角函数，并填在题中横线上：
（1）tan$\frac{3}{5}$π=-tan$\frac{2π}{5}$；
（2）tan100°21′=-tan79°39′；
（3）tan$\frac{31}{36}$π=-tan$\frac{5π}{36}$；
（4）tan324°32′=-tan35°28′．
16．根据下列条件，确定数列{an}的通项公式
（1）a1=1，an+1=3an+2 
（2）a1=1，an+1=（n+1）an 
（3）a1=2，an+1=an+ln（1+$\frac{1}{n}$）
13．已知函数f（x）=xlnx．
（Ⅰ）试求曲线y=f（x）在点（e，f（e））处的切线方程；
（Ⅱ）若x＞1，试判断方程f（x）=（x-1）（ax-a+1）的解的个数．
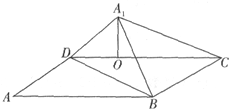20．如图，将矩形ABCD沿对角线BD把△ABD折起，使A点移到A1点，且A1在平面BCD上的射影O恰好在CD上．
（Ⅰ）求证：BC⊥A1D；
（Ⅱ）求证：平面A1CD⊥平面A1BC；
（Ⅲ）若AB=10，BC=6，求三棱锥A1-BCD的体积．
10．平面向量$\overrightarrow{{a}_{1}}$，$\overrightarrow{{a}_{2}}$，$\overrightarrow{{a}_{3}}$，…，$\overrightarrow{{a}_{8}}$都为单位向量，且满足$\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$=0（i=1，2，3，…，7），|$\overrightarrow{{a}_{1}}$+$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{3}}$+…+$\overrightarrow{{a}_{8}}$|的所有可能的不同值共有（　　）个．
A．5B．6C．7D．8
17．复数z=|$\sqrt{3}$-i|+i（i为虚数单位），则复数z的共轭复数为（　　）
A．2-iB．2+iC．4-iD．4+i
14．设函数f（x）=lnx+$\frac{1}{2}$x2-2x．
（Ⅰ）证明f（x）有唯一零点；
（Ⅱ）设g（x）=$\frac{1}{3}$x3-$\frac{1}{x}$-2af（x）-2x，若g（x）是增函数，求A的最大值．
15．已知直线l：x-y+c=0（c∈R），⊙M：（x-2）2+（y-2）2=1，直线l把⊙M分成两段圆弧，弧长之比为λ，其中$\frac{1}{2}$＜λ＜1，则c={c|-$\frac{\sqrt{2}}{2}$＜c＜$\frac{\sqrt{2}}{2}$，且 c≠0}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网