题目内容
(5分)(2011•天津)已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,﹣π<φ≤π.若函数f(x)的最小正周期为6π,且当x= 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
| A.f(x)在区间[﹣2π,0]上是增函数 | B.f(x)在区间[﹣3π,﹣π]上是增函数 |
| C.f(x)在区间[3π,5π]上是减函数 | D.f(x)在区间[4π,6π]上是减函数 |
A
解析试题分析:由函数f(x)的最小正周期为6π,根据周期公式可得ω=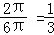 ,且当x=
,且当x= 时,f(x)取得最大值,代入可得,2sin(
时,f(x)取得最大值,代入可得,2sin(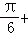 φ)=2,结合已知﹣π<φ≤π可得φ=
φ)=2,结合已知﹣π<φ≤π可得φ=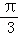 可得
可得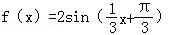 ,分别求出函数的单调增区间和减区间,结合选项验证即可
,分别求出函数的单调增区间和减区间,结合选项验证即可
解:∵函数f(x)的最小正周期为6π,根据周期公式可得ω= ,
,
∴f(x)=2sin(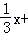 φ),
φ),
∵当x=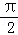 时,f(x)取得最大值,∴2sin(
时,f(x)取得最大值,∴2sin( φ)=2,
φ)=2,
∵﹣π<φ≤π,∴φ=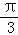 ,∴
,∴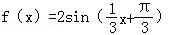 ,
,
由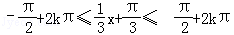 可得函数的单调增区间:
可得函数的单调增区间: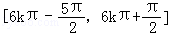 ,
,
由 可得函数的单调减区间:
可得函数的单调减区间: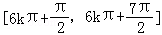 ,
,
结合选项可知A正确,
故选A.
点评:本题主要考查了利用函数的部分图象求解函数的解析式,还考查了函数y=Asin(ωx+φ)(A>0,ω>0)的单调区间的求解,属于对基础知识的考查.

练习册系列答案
相关题目
已知角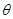 的顶点为坐标原点,始边为
的顶点为坐标原点,始边为 轴的非负半轴,若
轴的非负半轴,若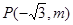 是角
是角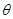 终边上的一点,且
终边上的一点,且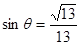 ,则
,则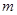 的值为( )
的值为( )
A. | B.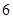 | C. 或 或 | D.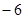 或 或 |
函数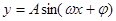 在一个周期内的图象如下,此函数的解析式为( )
在一个周期内的图象如下,此函数的解析式为( )
A.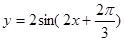 | B.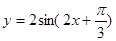 |
C.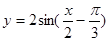 | D.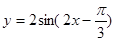 |
角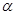 终边上有一点
终边上有一点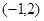 ,则下列各点中在角
,则下列各点中在角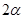 的终边上的点是 ( )
的终边上的点是 ( )
A.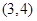 | B.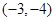 | C.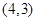 | D.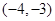 |
已知函数f(x)=sin(x+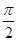 ),g(x)=cos(x-
),g(x)=cos(x-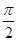 ),则下列结论中正确的是( )
),则下列结论中正确的是( )
A.函数y=f(x)·g(x)的最小正周期为2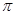 |
| B.函数y=f(x)·g(x)的最大值为1 |
C.将函数y=f(x)的图象向左平移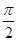 单位后得g(x)的图象 单位后得g(x)的图象 |
D.将函数y=f(x)的图象向右平移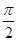 单位后得g(x)的图象 单位后得g(x)的图象 |
[2012·江西高考]若tanθ+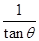 =4,则sin2θ=( )
=4,则sin2θ=( )
A. | B. | C. | D. |
[2014·荆州质检]将函数y=sin(2x+ )的图象向左平移
)的图象向左平移 个单位,再向上平移2个单位,则所得图象的一个对称中心是( )
个单位,再向上平移2个单位,则所得图象的一个对称中心是( )
A.( ,2) ,2) | B.( ,2) ,2) |
C.( ,2) ,2) | D.( ,2) ,2) |
 在[
在[ ]上的图像大致是( )
]上的图像大致是( )

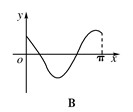


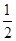 ,
,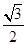 ),2α∈[0,2π),则tanα=( )
),2α∈[0,2π),则tanα=( )