题目内容
已知二面角α-PQ-β为60°,点A和B分别在平面α和平面β上,点C在棱PQ上,∠ACP＝∠BCP＝30°,CA=CB=a,求点B到平面α的距离.
解析:在β内作BD⊥PQ于D，连结AD.
∵∠BCD=∠ACD=30°,BC=AC=a,
∴△BCD≌△ACD.
于是AD⊥PQ，∠BDA为二面角α-PQ-β的平面角,
即∠BDA=60°,且AD=BD=
.
过B作BE⊥AD于E，
∵PQ⊥平面ABD，从而BE⊥α，
∴BE即为B点到平面α的距离.
在△ABD中，易知BE=
AD=
a.
练习册系列答案
相关题目
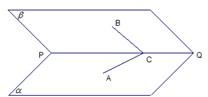已知二面角α-PQ-β为60°，点A和B分别在平面α和平面β内，点C在棱PQ上∠ACP=∠BCP=30°，CA=CB=a．
已知二面角α-PQ-β为
（2008•成都三模）如图，已知二面角α-PQ-β的大小为60°，点C为棱PQ一点，A∈β，AC=2，∠ACP=30°，则点A到平面α的距离为（ ）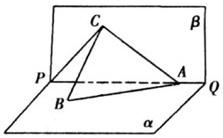
如图所示，PQ为平面α、β的交线，已知二面角α-PQ-β为直二面角，A∈PQ，B∈α，C∈β，CA=CB=kAB（k∈R*），∠BAP=45°．