题目内容
已知集合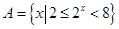 ,
,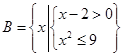 ,
,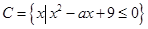
(1)若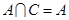 ,求
,求 的取值范围;
的取值范围;
(2)是否存在实数 使得
使得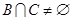 ?若存在求出
?若存在求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1) ;(2)
;(2)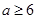 .
.
解析试题分析:(1)已知两个集合之间的关系求参数时,要明确集合中的元素,对子集是否为空集进行分类讨论,做到不漏解;(2)恒成立问题一般需转化为最值,利用单调性证明在闭区间的单调性.(3)一元二次不等式在 上恒成立,看开口方向和判别式.(4)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法:一是利用二次函数在区间上的最值来处理;二是分离参数,再去求函数的最值来处理,一般后者比较简单,对于恒成立的问题,常用到以下两个结论:(1)
上恒成立,看开口方向和判别式.(4)含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法:一是利用二次函数在区间上的最值来处理;二是分离参数,再去求函数的最值来处理,一般后者比较简单,对于恒成立的问题,常用到以下两个结论:(1)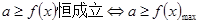 ,(2)
,(2)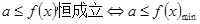
试题解析:(1)因为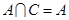 ,所以
,所以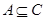 ,
,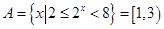 ,
,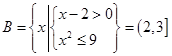 ,
,
法一:转化恒成立的不等式 也就是当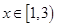 时,不等式
时,不等式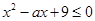 恒成立,即
恒成立,即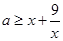 恒成立,令
恒成立,令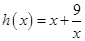 ,则
,则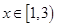 时
时 为减函数,故
为减函数,故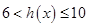 ,所以
,所以 ,即
,即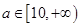 ; 7分
; 7分
法二:数形结合 令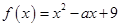 ,则
,则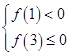 ,得
,得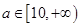 ; 7分
; 7分
(2)因为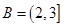 ,所以要使
,所以要使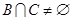 ,只要
,只要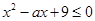 能成立,也就是
能成立,也就是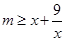 能成立,只要
能成立,只要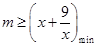 即可,由(1)知
即可,由(1)知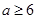 ,即
,即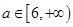 . 13分
. 13分
考点:(1)集合间的基本关系;(2)利用最值证明恒成立问题.

练习册系列答案
相关题目
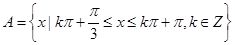 ,
,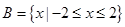 ,则
,则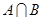 =______
=______ 是它的子集,
是它的子集, ;(2)若
;(2)若 =B,求
=B,求 的值;(3)若
的值;(3)若
 ,求
,求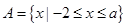 ,
,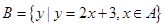 ,
,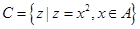 ,且
,且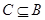 ,求
,求 的取值范围.
的取值范围. 的值域为集合A,函数
的值域为集合A,函数 的定义域为集合B.
的定义域为集合B. ,求实数a的取值范围.
,求实数a的取值范围.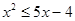 的解集为
的解集为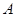 .
.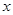 的不等式
的不等式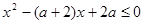 的解集为
的解集为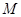 ,若
,若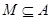 ,求实数
,求实数 的取值范围.
的取值范围. <n≤
<n≤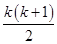 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*).对于l∈N*,定义集合Pl={n|Sn是an的整数倍,n∈N*,且1≤n≤l}.
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*).对于l∈N*,定义集合Pl={n|Sn是an的整数倍,n∈N*,且1≤n≤l}.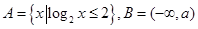 ,若
,若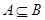 ,则实数
,则实数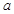 的取值范围是
的取值范围是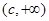 ,其中
,其中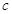 = ;
= ;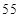 人,其中体育爱好者
人,其中体育爱好者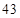 人,音乐爱好者
人,音乐爱好者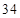 人,还有
人,还有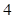 人既不爱好体育也不爱好音乐,则该班既爱好体育又爱好音乐的人数为 人
人既不爱好体育也不爱好音乐,则该班既爱好体育又爱好音乐的人数为 人