题目内容
14．已知数列{an}的通项公式an=n2-7n-8．（1）数列中有多少项为负数？
（2）数列{an}是否有最小项？若有，求出其最小项．
分析 （1）由an=n2-7n-8＜0，解得即可得出；
（2）an=n2-7n-8=$（n-\frac{7}{2}）^{2}$-$\frac{81}{4}$，利用二次函数的单调性即可得出．
解答 解：（1）由an=n2-7n-8＜0，解得1≤n＜8，因此数列中有7项为负数．
（2）∵an=n2-7n-8=$（n-\frac{7}{2}）^{2}$-$\frac{81}{4}$．
∴当n=3或4时，an取得最小值，
即a3=a4=-20，
故数列{an}有最小项为a3，a4，且a3=a4=-20．
点评 本题考查了数列的通项公式、二次函数的单调性，考查了计算能力，属于基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
4．设A={x|y=$\sqrt{2x-1}$，x∈R}，B={x|x2-3x-18＜0}，则A∩B=（ ）
| A． | （$\frac{1}{2}$，6） | B． | （$\frac{1}{2}$，3） | C． | [$\frac{1}{2}$，6） | D． | [$\frac{1}{2}$，3） |
5．函数f（x）=ln（x2-2x-3）的单调递减区间为（ ）
| A． | （-∞，1） | B． | （1，+∞） | C． | （-∞，-1） | D． | （3，+∞） |
1．抛物线x2=-2y的焦点坐标是（ ）
| A． | （-1，0） | B． | （1，0） | C． | $（0，-\frac{1}{2}）$ | D． | $（0，\frac{1}{2}）$ |
如图，已知直线l：y=kx-2与抛物线C：x2=-2py（p＞0）交于A，B两点，线段AB的中点坐标为（-2，-6）．
如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米．当水位上涨，水面宽为2米时，拱顶到水面的距离为0.5米．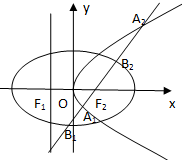
设抛物线C1：y2=4x的准线与x轴交于点F1，焦点为F2；以F1，F2为焦点，离心率为$\frac{1}{2}$的椭圆记作C2