题目内容
(理)已知球面上有A、B、C三点,AB=AC=2,BC=2| 2 |
分析:由题意可知三角形ACB是直角三角形,球心到平面ABC的距离为1,可求出球的半径,然后求球的表面积.
解答:解:由题意 AB=AC=2,BC=2
,
可知∠BAC=90°,球心到平面ABC的距离为1,
正好是球心到BC的中点的距离,
所以球的半径是:R=
球的表面积是:4πR2=12π.
故答案为:12π.
| 2 |
可知∠BAC=90°,球心到平面ABC的距离为1,
正好是球心到BC的中点的距离,
所以球的半径是:R=
| 3 |
球的表面积是:4πR2=12π.
故答案为:12π.
点评:本题考查球的内接体问题,考查学生空间想象能力,是中档题.确定三角形ABC的形状以及利用球半径与球心O到平面ABC的距离的关系,是解好本题的前提.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 ,球心到平面ABC的距离为1,则球的表面积为________.
,球心到平面ABC的距离为1,则球的表面积为________.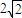 ,球心到平面ABC的距离为1,则球的表面积为 .
,球心到平面ABC的距离为1,则球的表面积为 .