题目内容
如图2-4-13,已知C点在⊙O直径BE的延长线上,CA切⊙O于A点,∠ACB的平分线CD交AE于F点,交AB于D点.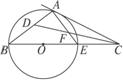
图2-4-13
(1)求∠ADF的度数.
(2)若∠ACB的度数为y度,∠B的度数为x度,那么y与x之间有怎样的关系?试写出你的猜测并给出证明.
(3)若AB=AC,求AC∶BC.
思路分析:(1)中由AC为⊙O切线可得∠B=∠EAC,由CD平分∠ACB可得∠ACD=∠DCB,根据三角形外角定理,得到∠ADF=∠AFD,建立等腰三角形,再由顶角求底角;(2)中则利用三角形内角和定理得到方程,获得关系;(3)中求线段的比值,利用△ACE∽△ABC可得.
解:(1)∵AC为⊙O切线,
∴∠B=∠EAC.
∵CD平分∠ACB,∴∠ACD=∠DCB.
∴∠B+∠DCB=∠EAC+∠ACD,即∠ADF=∠AFD.
∵BE为⊙O直径,∴∠DAE=90°.
∴∠ADF=![]() (180°-∠DAE)=45°.
(180°-∠DAE)=45°.
(2)∵∠B=∠EAC,∠B+∠BAC+∠ACB=180°,
∴x+90+x+y=180.∴y=90-2x.
∵0<∠B<∠ADC,∴0<x<45.
∴y与x的函数关系式是y=90-2x,其中x的取值范围是0<x<45.
(3)∵∠B=∠EAC,∠ACB=∠ACB,
∴△ACE∽△ABC.∴![]() .
.
∵AB=AC,∴∠B=∠ACB,即x=y.
又∵y=90-2x,∴x=90-2x,x=30.
∴在Rt△ABE中,![]() =tan∠ABE=tan30°=
=tan∠ABE=tan30°=![]() .
.

练习册系列答案
相关题目
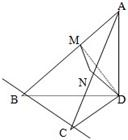 如图所示,直线AD、CD、BC两两垂直,且AD与BC不在同一平面内.已知BC=3,CD=4,AB=13,点M、N分别为线段AB、AC的中点.
如图所示,直线AD、CD、BC两两垂直,且AD与BC不在同一平面内.已知BC=3,CD=4,AB=13,点M、N分别为线段AB、AC的中点. 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.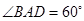 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线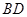 翻折,使点
翻折,使点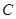 翻折到点
翻折到点 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.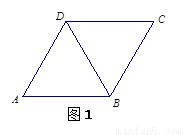

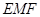 ;
;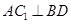
 时,求线段AC1 的长.
时,求线段AC1 的长.