题目内容
如图2-4,已知Rt△ABC中,∠B=90°,AC=13,AB=5,O是AB上的点,以O为圆心,OB为半径作⊙O.(1)当OB=2.5时,⊙O交AC于点D,求CD的长.
(2)当OB=2.4时,AC与⊙O的位置关系如何?试证明你的结论.
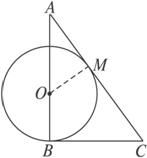
图2-4
思路分析:求CD的长容易想到利用圆幂定理.其中AC已知,只需求BC并证BC为切线即可.
解:(1)在Rt△ABC中,BC=![]() =12.
=12.
∵∠B=90°,OB为半径,
∴BC是⊙O切线.
又AB=5,OB=2.5,
∴OA=2.5,即A在圆上.
由切割线定理,得BC2=CD·AC.
∴CD=![]() .
.
(2)当OB=2.4时,AC是⊙O的切线,如图2-5.

图2-5
证明:过O作OM⊥AC于M,则△AOM∽△ACB.
∴![]() .
.
∴OM=2.4,
即点O到AC的距离等于⊙O的半径.
∴AC切⊙O于点M.

练习册系列答案
相关题目
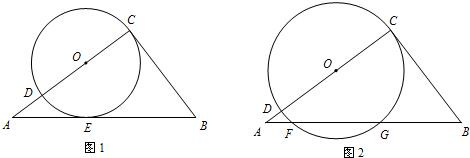

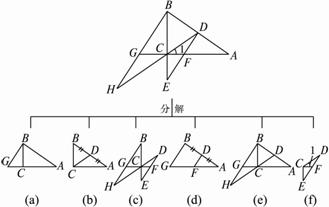
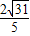 ,求⊙O的半径.
,求⊙O的半径.