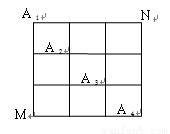
题目内容
 如图,在某城市中,
如图,在某城市中, 两地之间有整齐的方格形道路网,其中
两地之间有整齐的方格形道路网,其中 、
、 、
、 、
、 是道路网中位于一条对角线上的4个交汇处.今在道路网
是道路网中位于一条对角线上的4个交汇处.今在道路网 处的甲、乙两人分别要到
处的甲、乙两人分别要到 处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达
处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达 为止.
为止.
(1)求甲经过 到达N的方法有多少种;
到达N的方法有多少种;
(2)求甲、乙两人在 处相遇的概率;
处相遇的概率;
(3)求甲、乙两人相遇的概率.
【答案】
解:(1)甲经过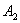 ,可分为两步:
,可分为两步:
第一步,甲从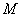 经过
经过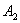 的方法数为
的方法数为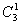 种;
种;
第二步,甲从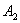 到
到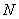 的方法数为
的方法数为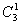 种;
种;
所以甲经过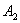 到达
到达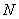 的方法数为
的方法数为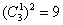 种.………………………………2分
种.………………………………2分
(2)由(1)知,甲经过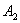 的方法数为
的方法数为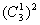 ;乙经过
;乙经过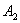 的方法数也为
的方法数也为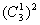 .
.
所以甲、乙两人在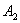 处相遇的方法数为
处相遇的方法数为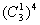 =81;
=81;
甲、乙两人在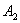 处相遇的概率为
处相遇的概率为 .………………………6分
.………………………6分
(3)甲、乙两人沿最短路径行走,只可能在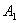 、
、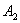 、
、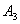 、
、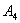 处相遇,他们在
处相遇,他们在 相遇的走法有
相遇的走法有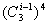 种方法;
种方法;
所以: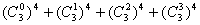 =164
=164
故甲、乙两人相遇的概率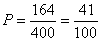 .
.
答:(1)甲经过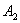 到达
到达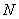 的方法数为
的方法数为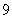 种;
种;
(2)甲、乙两人在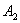 处相遇的概率为
处相遇的概率为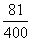 ;
;
(3)甲、乙两人相遇的概率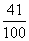 .
………………………10分
.
………………………10分

练习册系列答案
相关题目
 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到N,M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到N,M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.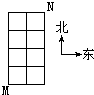 如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有( )
如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有( )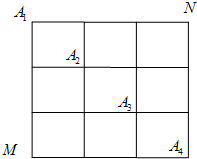 如图,在某城市中,M,N两地之间有整齐的方格形道路网,其中A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处.今在道路网M,N处的甲、乙两人分别要到N,M处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达N,M为止.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,其中A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处.今在道路网M,N处的甲、乙两人分别要到N,M处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达N,M为止. (1)求甲经过
(1)求甲经过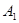 、
、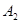 、
、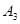 、
、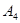 是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到N、M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.
是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到N、M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.