题目内容
已知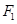 、
、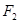 分别是椭圆
分别是椭圆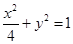 的左、右焦点.
的左、右焦点.
(1)若 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,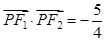 ,求点
,求点 的坐标;
的坐标;
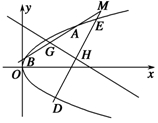
(2)设过定点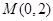 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且
,且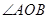 为锐角(其
为锐角(其
中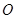 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率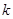 的取值范围.
的取值范围.
(1)点 的坐标为
的坐标为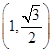 ;(2)直线
;(2)直线 的斜率
的斜率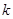 的取值范围是
的取值范围是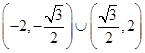 .
.
解析试题分析:(1)设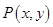 ,由椭圆方程可表示出
,由椭圆方程可表示出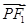 、
、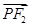 ,又
,又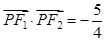 ,即可求点
,即可求点 的坐标;
的坐标;
(2)显然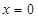 不满足题意,所直线的斜率存在,可设
不满足题意,所直线的斜率存在,可设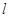 的方程为
的方程为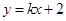 ,与椭圆方程联立后用韦达定理表示出
,与椭圆方程联立后用韦达定理表示出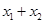 、
、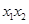 ;又
;又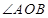 为锐角,
为锐角,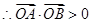 ,进而可解出
,进而可解出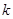 的取值范围.
的取值范围.
试题解析:(1)因为椭圆方程为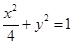 ,知
,知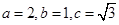 ,
,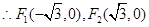 ,
,
设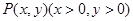 ,则
,则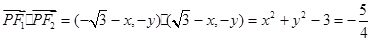 ,
,
又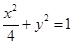 ,联立
,联立 ,解得
,解得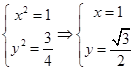 ,
,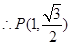 6分
6分
(2)显然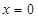 不满足题意,所直线的斜率存在,可设
不满足题意,所直线的斜率存在,可设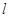 的方程为
的方程为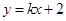 ,
,
设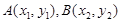 ,联立
,联立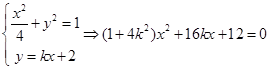
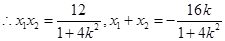 , 8分
, 8分
且△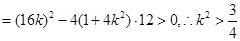 10分
10分
又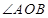 为锐角,
为锐角,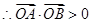 ,
,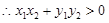 ,
,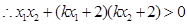 ,
,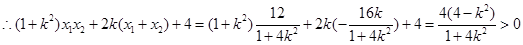
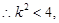 又
又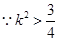 ,
,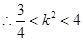 ,
, 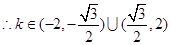 12分
12分
考点:直线与圆锥曲线的综合问题、设而不求思想.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
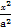 +
+ =1(a>b>0)的右焦点为F(1,0),且点(-1,
=1(a>b>0)的右焦点为F(1,0),且点(-1,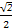 )在椭圆C上.
)在椭圆C上. ,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明: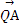 ·
·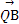 为定值.
为定值.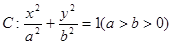 的离心率为
的离心率为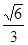 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为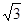 .
.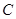 的方程;
的方程;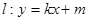 与椭圆
与椭圆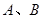 两点,坐标原点
两点,坐标原点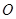 到直线
到直线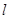 的距离为
的距离为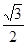 ,求
,求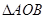 面积的最大值.
面积的最大值. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为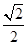 ,一条准线l:x=2.
,一条准线l:x=2.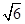 ,求圆D的方程;
,求圆D的方程; ,且过点M
,且过点M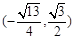 。
。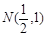 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.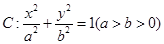 的离心率是
的离心率是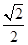 ,
,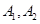 分别是椭圆
分别是椭圆 的左、右两个顶点,点
的左、右两个顶点,点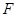 是椭圆
是椭圆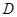 是
是 轴上位于
轴上位于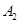 右侧的一点,且满足
右侧的一点,且满足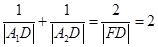 .
.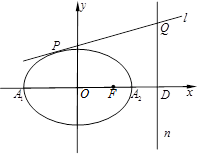
 ,再作直线
,再作直线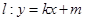 与椭圆
与椭圆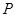 ,直线
,直线 交直线
交直线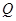 .求证:以线段
.求证:以线段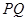 为直径的圆恒过定点,并求出定点的坐标.
为直径的圆恒过定点,并求出定点的坐标.
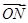 =
=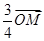 ,O为坐标原点.
,O为坐标原点.