题目内容
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上,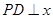 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(1)求曲线 的方程;
的方程;
(2)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分。
轴平分。
【答案】
(1)
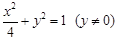
(2) 略
【解析】解:(1)设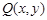 为曲线
为曲线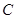 上的任意一点,则点
上的任意一点,则点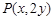 在圆
在圆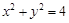 上,
上,
∴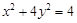 ,曲线
,曲线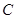 的方程为
的方程为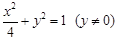 .
.
(2)设点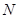 的坐标为
的坐标为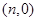 ,直线
,直线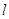 的方程为
的方程为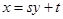 ,
,
代入曲线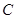 的方程
的方程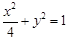 ,可得
,可得
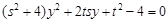 ,
,
∵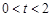 ,∴
,∴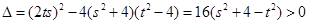 ,
,
∴直线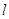 与曲线
与曲线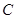 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆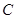 的内部得到此结论)
的内部得到此结论)
设点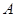 ,
,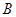 的坐标分别
的坐标分别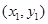 ,
, 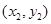 ,
,
则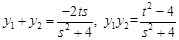 ,
,
要使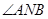 被
被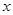 轴平分,只要
轴平分,只要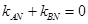 ,
,
即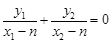 ,
,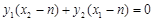 ,
,
也就是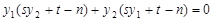 ,
,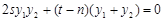 ,
,
即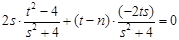 ,即只要
,即只要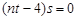
当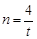 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而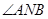 总能被
总能被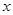 轴平分.
轴平分.
所以在x轴上存在定点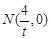 ,使得
,使得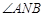 总能被
总能被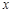 轴平分.
轴平分.

练习册系列答案
相关题目
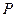 为圆
为圆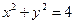 上的动点,且
上的动点,且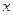 轴上,
轴上,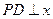 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点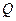 的轨迹为曲线
的轨迹为曲线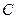 ,过定点
,过定点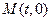
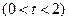 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线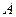 、
、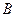 两点。
两点。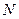 ,使得
,使得 总能被
总能被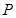 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上,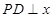 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线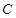 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被 为曲线
为曲线 在圆
在圆 上,
上, ,曲线
,曲线
 ,直线
,直线 , ………………3分
, ………………3分  ,可得
,可得 
 ,∴
,∴
 ,
,  ,则
,则 ,
,  得到。
得到。 ,
, ,
, , ………………10分
, ………………10分 ,
, ,
,  ,即只要
,即只要 ………………12分
………………12分  时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 ,使得
,使得 总能被
总能被 轴平分
轴平分