题目内容
11．已知集合M={m|$\frac{m-4}{2}$∈Z}，P={p|$\frac{p+3}{2}$∈Z}，则M∩P=∅．分析 根据已知分析可得M为偶数集，P是奇数集，进而根据集合交集的定义，得到答案．
解答 解：∵集合M={m|$\frac{m-4}{2}$∈Z}，P={p|$\frac{p+3}{2}$∈Z}，
∴M为偶数集，P是奇数集，
∴M∩P=∅，
故答案为：∅
点评 本题考查的知识点是集合交集及其运算，难度不大，属于基础题．
练习册系列答案
相关题目
2．
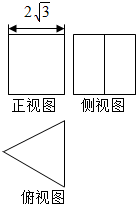一个体积为12$\sqrt{3}$的正三棱柱（底面为正三角形，且侧棱垂直于底面的棱柱）的三视图如图所示，则该三棱柱的侧视图的面积为（ ）
一个体积为12$\sqrt{3}$的正三棱柱（底面为正三角形，且侧棱垂直于底面的棱柱）的三视图如图所示，则该三棱柱的侧视图的面积为（ ）| A． | 6$\sqrt{3}$ | B． | 8 | C． | 8$\sqrt{3}$ | D． | 12 |
8．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，左顶点为A，点B（0，b），若线段AF1（不含端点）上存在点P，使得以PF2为直径的圆经过点B，则双曲线C的离心率的取值范围是（ ）
| A． | （1，$\frac{1+\sqrt{5}}{2}$） | B． | （$\frac{1+\sqrt{5}}{2}$，+∞） | C． | （$\sqrt{2}$，$\frac{1+\sqrt{5}}{2}$） | D． | （$\sqrt{2}$，+∞） |