题目内容
比较大小,正确的是( )A.sin(-5)<sin3<sin5
B.sin(-5)>sin3>sin5
C.sin3<sin(-5)<sin5
D.sin3>sin(-5)>sin5
【答案】分析:因为角5的终边位于第四象限,所以sin5是负值,然后利用诱导公式找到(0,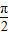 )内与-5和3正弦值相等的角,根据第一象限正弦函数的单调性可得结论.
)内与-5和3正弦值相等的角,根据第一象限正弦函数的单调性可得结论.
解答:解:因为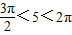 ,
,
所以sin5<0.
而sin(-5)=sin(2π-5)
sin3=sin(π-3)
由0<π-3<2π-5<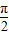 ,
,
所以,sin(2π-5)>sin(π-3)>0.
综上,sin(-5)>sin(3)>sin5.
故选B.
点评:本题考查了不等关系与不等式,考查了三角函数的诱导公式,同时考查了三角函数的单调性,属基础题.
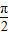 )内与-5和3正弦值相等的角,根据第一象限正弦函数的单调性可得结论.
)内与-5和3正弦值相等的角,根据第一象限正弦函数的单调性可得结论.解答:解:因为
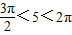 ,
,所以sin5<0.
而sin(-5)=sin(2π-5)
sin3=sin(π-3)
由0<π-3<2π-5<
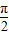 ,
,所以,sin(2π-5)>sin(π-3)>0.
综上,sin(-5)>sin(3)>sin5.
故选B.
点评:本题考查了不等关系与不等式,考查了三角函数的诱导公式,同时考查了三角函数的单调性,属基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目