题目内容
如图以椭圆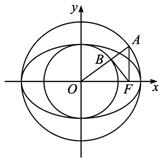
(Ⅰ)证明:c2=ab,并求直线BF与y轴的交点M的坐标;
(Ⅱ)设直线BF交椭圆于P、Q两点,证明![]() ·
·![]() =
=![]() b2.
b2.
(Ⅰ)证明:由题设条件知,Rt△OFA∽Rt△OBF,故![]() ,即
,即![]() =
=![]() ,因此c2=ab,
,因此c2=ab,
解:在Rt△OFA中,FA=![]() =b,于是直线OA的斜率kOA=
=b,于是直线OA的斜率kOA=![]() ,则直线BF的方程为y=-
,则直线BF的方程为y=-![]() (x-c),令x=0,则y=
(x-c),令x=0,则y=![]() =a,∴直线BF与y轴的交点为M(0,a).
=a,∴直线BF与y轴的交点为M(0,a).
(Ⅱ)证明:由(Ⅰ),得直线BF的方程为y=kx+a ①
且k2=![]() =
=![]() . ②
. ②
由已知,设P(x1,y1),Q(x2,y2),则它们的坐标满足方程组 ③
③
由方程组③消去y,整理得(b2+a2k2)x2+2a3kx+a4-a2b2=0, ④
由式①、②和④
x1·x2= ,
,
由方程组③消去x,并整理得(b2+a2k2)y2-2ab2y+a2b2-a2b2k2=0. ⑤
由式②和⑤,y1·y2= ,
,
综上得,![]() ·
·![]() =x1x2+y1y2=
=x1x2+y1y2=![]() +
+![]() ,
,
注意到a2-ab+b2=a2-c2+b2=2b2,得
![]() ·
·![]() =
=![]() =
=![]() (a2-ab)=
(a2-ab)=![]() b2.
b2.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 +
+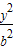 =1(a>b>0)上的点到左焦点为F的最大距离是
=1(a>b>0)上的点到左焦点为F的最大距离是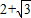 ,已知点M(1,e)在椭圆上,其中e为椭圆的离心率.
,已知点M(1,e)在椭圆上,其中e为椭圆的离心率.
 +
+ =1(a>b>0)上的点到左焦点为F的最大距离是
=1(a>b>0)上的点到左焦点为F的最大距离是 ,已知点M(1,e)在椭圆上,其中e为椭圆的离心率.
,已知点M(1,e)在椭圆上,其中e为椭圆的离心率.
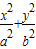 =1(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且
=1(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且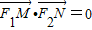 .
. ,MN的最小值为
,MN的最小值为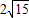 ,求椭圆方程.
,求椭圆方程.
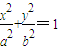 (a>b>0)过点
(a>b>0)过点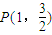 ,其左、右焦点分别为F1,F2,离心率
,其左、右焦点分别为F1,F2,离心率 ,M,N是椭圆右准线上的两个动点,且
,M,N是椭圆右准线上的两个动点,且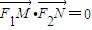 .
.